Контакты

Случайная статья

Производная показательной функции

Стр 1 из 2Следующая ⇒

Производная показательной функции

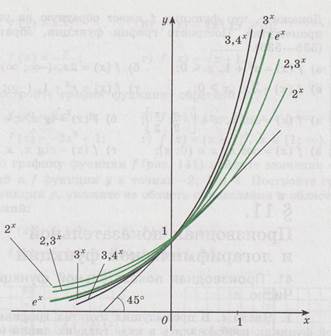Нарисуем несколько графиков функции 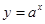для а, равного 2; 2,3; 3; 3,4 и проведём к ним касательные в точке с абсциссой 0. Углы наклона этих касательных к оси абсцисс приблизительно равны 35⁰, 40⁰, 48⁰ и 51⁰ соответственно, т. е. с возрастанием а угловой коэффициент касательной к графику функции 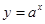в точке М(0; 1) постепенно увеличивается от tg35⁰ до tg51⁰. Увеличивая а от 2 до 3, мы найдём такое значение а, при котором угловой коэффициент соответствующей касательной равен 1 (т. е. угол наклона равен 45⁰).

Существует такое число большее 2 и меньшее 3 (это число обозначается буквой е), что показательная функция 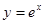в точке 0 имеет производную, равную 1.

е = 2,718281…

Функцию 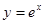называют экспонентой.

Теорема 1. Функция 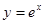дифференцируема в каждой точке области определения, и .

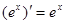Пример 1.Найти производную функции .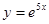

.

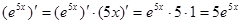Натуральным логарифмом (обозначается ln) называется логарифм по основанию е: .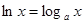

По основному логарифмическому тождеству, для любого положительного числа 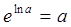. Поэтому 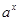может быть записано в виде .

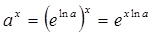Теорема 2. Показательная функция 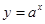дифференцируема в каждой точке области определения, и .

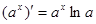Пример 2.Найти производные функци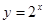й и .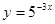

Решение.

;

.

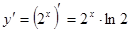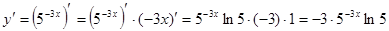Пример 3.Найти производную функции .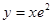

12 Следующая ⇒

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.