
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Результаты расчета
Результаты расчета
В расчетах параметры фаз взяты при температуре среды 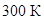 . Для воздуха:
. Для воздуха: 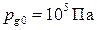 ,
, 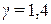 ,
, 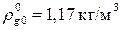 ,
, 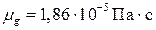 . Для песчаника:
. Для песчаника: 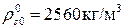 ,
, 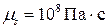 ,
, 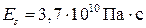 . Для воды:
. Для воды: 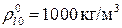 ,
, 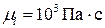 ,
, 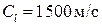 .
.
Пузырьковая жидкость является средой с уникальными акустическими свойствами [17]. Добавление в жидкость пузырьков газа, объемном содержание которых порядка 1-2% кардинально меняет его акустические свойства. Из-за аномальной сжимаемости скорость распространения звуковых волн может уменьшиться до значения 100 м/с, кроме этого, из-за неравновесного теплообмена между жидкостью и газом и акустической разгрузкой [17]. В [17] получено дисперсионное уравнение:
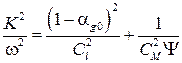 (9)
(9)
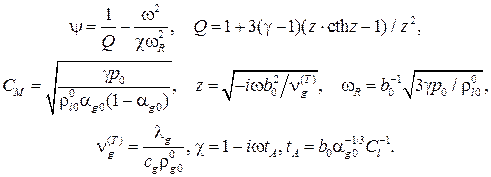
На рисунке 2 показаны зависимости коэффициента затухания 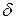 и фазовой скорости
и фазовой скорости 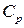 от частоты ω для случая воды с пузырьками воздуха при
от частоты ω для случая воды с пузырьками воздуха при 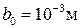 ,
, 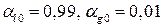 .
.
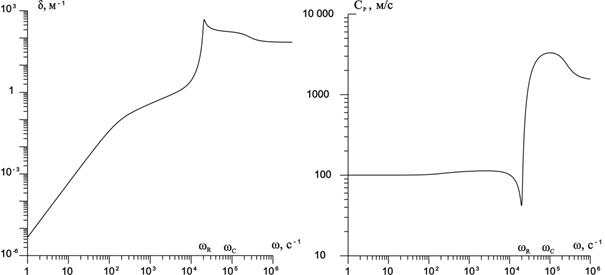
Рисунок 2. Зависимость фазовой скорости 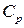 и коэффициента затухания
и коэффициента затухания 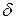 от частоты ω для случая воды с пузырьками воздуха при
от частоты ω для случая воды с пузырьками воздуха при 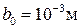 ,
, 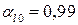 .
.
На этих графиках наблюдаются три характерных диапазона частот, где существенно различаются не только количественная, но и качественная картина дисперсионных кривых. Из анализа дисперсионного уравнения (9) следует, что эффект дисперсии звука в низкочастотной области 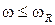 (
( 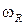 –частота собственных колебаний пузырьков, частота Миннаерта [1]) определяется межфазной температурной неравновесностью. В диапазоне частот
–частота собственных колебаний пузырьков, частота Миннаерта [1]) определяется межфазной температурной неравновесностью. В диапазоне частот 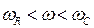 (
( 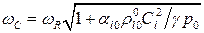 )коэффициент затухания и фазовая скорость принимают аномально высокие значения, поэтому эта зона частот соответствует зоне непропускания. Вне этого диапазона (
)коэффициент затухания и фазовая скорость принимают аномально высокие значения, поэтому эта зона частот соответствует зоне непропускания. Вне этого диапазона ( 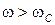 ) скорость звука и коэффициент затухания стремятся к определенным значениям. Отметим, что величина, обратная декременту затухания, соответствует расстоянию, на котором амплитуда волн уменьшается в e раз, где e–основание натурального логарифма. Из рисунка 2 видно, что при частоте равной частоте собственных колебаний пузырьков фазовая скорость звука минимальна составляет 60 м/с, а значение логарифмического декремента затухания максимальна.
) скорость звука и коэффициент затухания стремятся к определенным значениям. Отметим, что величина, обратная декременту затухания, соответствует расстоянию, на котором амплитуда волн уменьшается в e раз, где e–основание натурального логарифма. Из рисунка 2 видно, что при частоте равной частоте собственных колебаний пузырьков фазовая скорость звука минимальна составляет 60 м/с, а значение логарифмического декремента затухания максимальна.
Особым свойством насыщенной газом или жидкостью пористой среды является то, что в такой среде, в отличие от однофазной, могут распространяться упругие продольные волны двух типов (быстрая и медленная), а также поперечная волна [2]. В работе [18] для схемы пористой среды, представленной на рисунке 1 получено дисперсионное соотношение для пористой среды полностью насыщенной жидкостью, следующего вида:
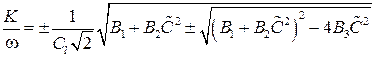 , (10)
, (10)
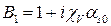 ,
, 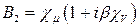 ,
, 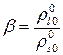 ,
, 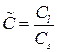 ,
, 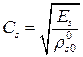 ,
, 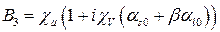 ,
, 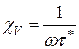 ,
, 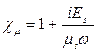 ,
,
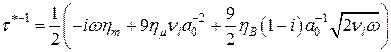 ,
, 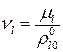 .
.
 – фазовые скорости волны в жидкости и в скелете пористой среды соответственно.
– фазовые скорости волны в жидкости и в скелете пористой среды соответственно.
На рисунке 3 показаны зависимости коэффициента затухания 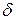 и фазовой скорости
и фазовой скорости 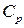 «быстрой» (штриховые линии) и «медленной» (сплошные линии) волн от частоты ω, построенные на основе выражения (10).
«быстрой» (штриховые линии) и «медленной» (сплошные линии) волн от частоты ω, построенные на основе выражения (10).
Из рисунка 3 видно, что коэффициент затухания для обоих типов волн увеличивается с увеличением частоты, кроме этого, коэффициент затухания «быстрой» волны для частот 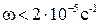 больше чем коэффициент затухания «медленной» волны. Также следует, что для частот
больше чем коэффициент затухания «медленной» волны. Также следует, что для частот 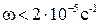 гармоническая волна затухает на расстоянии порядка 100 м. Из графика зависимости фазовой скорости от частоты следует, что для обеих типов волн с увеличением частоты скорости возрастают. Для частот ω >103 с-1оба типа волн и «медленна» и «быстрая» скорости волн стремятся к постоянным значениям. Скорость «медленной» волны стремится к скорости звука в воде, а скорость «быстрой» волны к скорости звука в песчанике.
гармоническая волна затухает на расстоянии порядка 100 м. Из графика зависимости фазовой скорости от частоты следует, что для обеих типов волн с увеличением частоты скорости возрастают. Для частот ω >103 с-1оба типа волн и «медленна» и «быстрая» скорости волн стремятся к постоянным значениям. Скорость «медленной» волны стремится к скорости звука в воде, а скорость «быстрой» волны к скорости звука в песчанике.
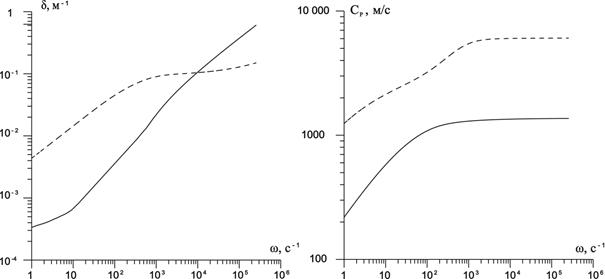
Рисунок 3. Зависимости коэффициента затухания 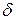 и фазовой скорости
и фазовой скорости 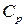 «быстрой» (пунктирные линии) и «медленной» (сплошные линии) волн от частоты ω для системы песчаник– вода. Характерные параметры пористой среды:
«быстрой» (пунктирные линии) и «медленной» (сплошные линии) волн от частоты ω для системы песчаник– вода. Характерные параметры пористой среды: 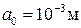 ,
, 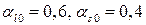 .
.
На рисунке 4 показаны зависимости коэффициента затухания 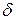 и фазовой скорости
и фазовой скорости 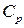 «быстрой» (штриховые линии) и «медленной» (сплошные линии) волн от частоты ω для случая, когда пузырьковая среда заполнена газожидкостной смесью.
«быстрой» (штриховые линии) и «медленной» (сплошные линии) волн от частоты ω для случая, когда пузырьковая среда заполнена газожидкостной смесью.
Из рисунка 4 видно, что характер зависимости для «медленной» волны для пористой среды заполненной пузырьковой смесью такой же, как для «свободной» пузырьковой жидкости, характерные диапазоны частот также разделяют «поведение» кривых коэффициента затухания и фазовой скорости. Коэффициент затухания «быстрой» волны до частоты ωC имеет такой же вид, как для случая пористой среды, насыщенной «чистой» жидкостью, а при частоте ω»ωC происходит резкое уменьшение коэффициента затухания, что соответствует неустойчивому состоянию системы. Кроме этого также отметим, что для частот 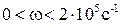 коэффициент затухания для «медленной» волны в пористой среде заполненной пузырьковой смесью больше чем коэффициент затухания звука в пузырьковой воде (рисунок 2). Скорость быстрой волны для пористой среды заполненной пузырьковой смесью увеличивается в диапазоне частот 0<ω<102c-1 до значения скорости звука в песчанике.
коэффициент затухания для «медленной» волны в пористой среде заполненной пузырьковой смесью больше чем коэффициент затухания звука в пузырьковой воде (рисунок 2). Скорость быстрой волны для пористой среды заполненной пузырьковой смесью увеличивается в диапазоне частот 0<ω<102c-1 до значения скорости звука в песчанике.
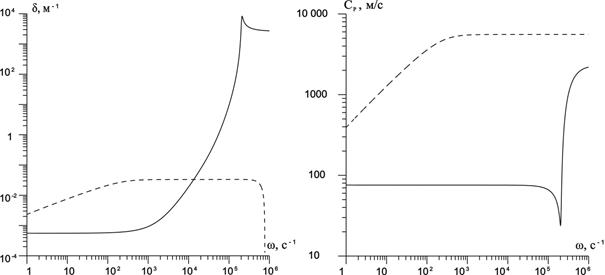
Рисунок 4. Зависимости коэффициента затухания 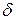 и фазовой скорости
и фазовой скорости 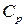 «быстрой» (пунктирные линии) и «медленной» (сплошные линии) волн от частоты ω для системы песчаник –пузырьковая жидкость. Характерные параметры системы (пористая среда+пузырьковая смесь)
«быстрой» (пунктирные линии) и «медленной» (сплошные линии) волн от частоты ω для системы песчаник –пузырьковая жидкость. Характерные параметры системы (пористая среда+пузырьковая смесь) 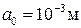 ,
, 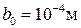 ,
, 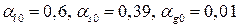 .
.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|