Введение. Основные уравнения

Введение

Исследование процессов распространения волн давления в насыщенных пористых средах связано не только с решением практических задач подводной акустики, сейсмики, защиты объектов, неразрушающего контроля и т.д., но и для понимания фундаментальных основ волновых процессов в таких средах. Обзор работ по динамике волн в пористых средах представлен в работах [1-6].

В пластовых жидкостях во многих случаях присутствует газ. Например, газожидкостная смесь в пористой среде образуется при кислотных обработках низкопроницаемых зон, при водогазовом воздействии на пласты и т.д. Поэтому представляется актуальным учитывать присутствие пузырьков газа при изучении волновых процессов в пористых средах насыщенных пузырьковой жидкостью.

Отметим работы, посвященные экспериментальному и теоретическому изучению динамики волн давления в пористых средах заполненных газожидкостной смесью.

В ряде работ В.Е. Донцова [7-9] на установке «ударная труба» экспериментально изучена эволюция и структура волн давления в пористой среде, насыщенной жидкостью с пузырьками газа. В качестве рабочей среды использовалась хаотическая упаковка из спеченных шариков оргстекла диаметром около 2 мм, запекаемых непосредственно в рабочем участке. Насыщающей жидкостью была вода, газом – воздух или углекислый газ. Пьезоэлектрические датчики располагались по длине рабочего участка. Они не касались скелета пористой среды и измеряли профиль волны давления в жидкости. Установлено, что затухание «медленной» волны в пористой среде, насыщенной жидкостью с пузырьками углекислого газа, меньше, чем в пористой среде, насыщенной жидкостью с пузырьками воздуха. Показано, что колебания пузырьков обусловливают осциллирующую структуру переднего фронта «медленной» волны давления. Шмельдерс с соавторами [10-11] экспериментально и теоретически исследовали эволюцию волн давления в пористой среде насыщенной пузырьковой жидкостью. Эксперименты проведены на ударной трубе. В качестве пористой среды использовались склеенные частицы песка или природный песчаник. Далее пористый образец насыщался пузырьковой жидкостью, которая готовилась в отдельной емкости. Особое внимание уделяется приготовлению однородной водно-воздушной смеси в порах обоих образцов. В дальнейшем эксперимент проводится для обоих образцов. Как и в работе [6] показано, что волна имеет осцилляционную структуру, связанную с наличием пузырьков. Обнаружены две продольные волны Био. Показано, волна в пористой среде насыщенной пузырьковой жидкостью имеет осцилляционную структуру, незначительное количество газа в жидкости, которая насыщает пористую среду существенно влияет на динамику волн давления. Динамика ударных волн в пористой среде, состоящей из частиц песка, склееных эпоксидной смолойэкспериментально и теоретически исследовано Гринтенем (vanderGrinten J.G.M.) в [12]. Рассмотрены три случая: поры полностью насыщенные водой, поры заполнены воздухом и поры содержат смесь воды и пузырьков воздуха. Показано, что ударную трубу можно использовать для изучения отражения высокочастотных компонент ударной волны от пористой среды. Получено хорошее соответствие между линейной теорией и экспериментом для случая насыщения пористой среды водой. Для частично насыщенной пористой среды, соответствие удовлетворительное.

В [13] экспериментально и теоретически исследуется распространение слабых ударных волн во влажном песке для различного содержания воды. Установлена немонотонная зависимость амплитуды волны, образующейся во влажной пористой среде, от степени водонасыщенности.

Теоретические исследования волновых процессов в насыщенных газожидкостной смесью пористых средах проводились в [14-16].

В [14] рассматривается задача о распространении продольных волн в насыщенной жидкостью пористой среде при наличии пузырьков газа. В линейном приближении построены зависимости коэффициента затухания и фазовой скорости волн Френкеля - Био первого и второго рода от частоты. Показано, что в окрестности резонансной частоты пузырьков продольные волны Френкеля - Био изменяют свой характер. Волна первого рода трансформируется из быстрой волны при низких частотах в медленную при высоких. Дисперсионная кривая волны второго рода состоит из двух ветвей - "низкочастотной" ветви, колебания которой обладают классическими свойствами, и "высокочастотной", которая является слабозатухающей высокоскоростной модой. Построены частотные зависимости отношения массовых скоростей газожидкостной смеси и пористой матрицы, а также возмущений напряжения в матрице и давления в смеси. Выявлено, что "высокочастотная" ветвь волны второго рода характеризуется сонаправленным движением газожидкостной смеси и пористой матрицы, а их массовые скорости близки, что объясняет низкое затухание данной моды колебаний. Получено аналитическое выражение для "граничной частоты", определяющей начало "высокочастотной" ветви дисперсионной кривой волны второго рода.

В работах [15-16] численно исследованы волновые процессы в пористой среде, насыщенной пузырьковой жидкостью, с учетом нелинейности колебаний пузырьков. Нелинейность учтена в уравнениях состояния газа и Рэлея – Ламба. Численное исследование в рамках нелинейной модели выполнено впервые. Получены дисперсионные зависимости. Проанализировано влияние свойств пористой среды и параметров пузырьковой жидкости на скорость и затухание деформационной и фильтрационной волн. Исследовано прохождение волны ступенчатого профиля из жидкости в пористую среду, насыщенную пузырьковой жидкостью. Изучено влияние параметров среды и интенсивности падающей волны на эволюцию волн в насыщенной пузырьковой жидкостью пористой среде. Результаты расчетов показывают хорошее качественное согласование с экспериментальными данными других авторов.

В данной работе теоретически исследуется распространение акустических волн в пористой среде насыщенной газожидкостной смесью.

Основные уравнения

При описании распространения акустических волн во в пористой среде, насыщенной пузырьковой смесью, примем следующие допущения: значения длин рассматриваемых волн намного больше размеров пор, радиуса пузырьков и расстояния между пузырьками; скорости жидкости и газа при прохождении волны равны 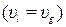. В качестве характерных размеров среды примем средний радиус пор 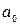, характерный размер пузырьков газа 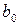(рис. 1).

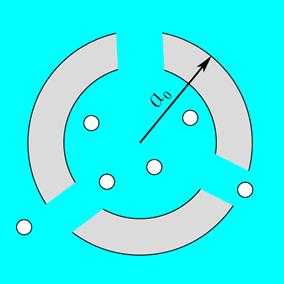
Рисунок 1. Ячейка пористой среды.

Запишем макроскопические линеаризованные уравнения массы для жидкости, газа в порах и скелета пористой среды в двухскоростном приближении и числа пузырьков [1,15,16]:

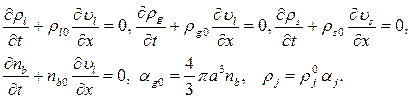(1)

Здесь 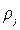, , 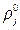, , 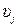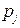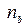– средняя по объему и средняя по фазе плотности, скорость, давление, объемные содержания и число пузырьков в единице объема. Дополнительный нижний индекс соответствует первоначальному невозмущенному состоянию.

Уравнения импульсов для жидкости содержащей пузырьки газа и для всей системы (жидкость+пористая среда) имеют следующий вид [15, 16]:

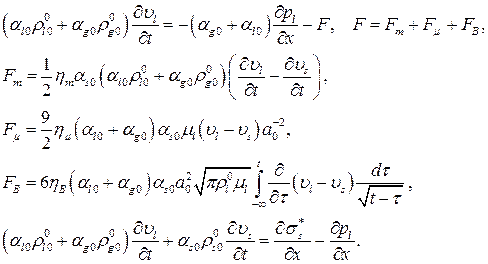(2)

Здесь 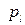– давление в жидкост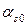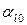и, , и 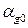– объемные содержания твердой, жидкой и газовой фаз соответственно, 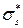– приведенное напряжение в скелете; 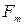– сила присоединенных масс, вызванная инерционным взаимодействием фаз, 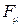– аналог силы вязкого трения Стокса, 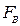– аналог силы Бассэ, проявляющейся при высоких частотах из-за нестационарности вязкого пограничного слоя около границы с твердой фазой, 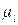– вязкость жидкости.

Для твердой и жидкой фаз принято линейное уравнение состояния в акустическом приближении, для скелета пористой среды примем модель Максвелла [5,6,15]:

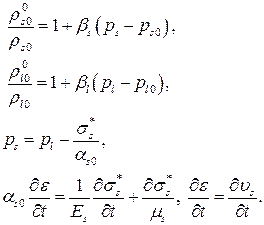(3)

Будем полагать, что газ в пузырьках сжимается адиабатически:

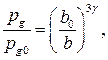(4)

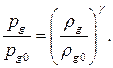(5)

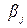–сжимаемость фаз. Здесь 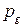– давление в газовой фазе.

Дополнительным нижним индексом (0) определены параметры, соответствующие невозмущенному состоянию, а параметры без индекса выражают малые возмущения параметров от равновесного значения; верхний индекс (0) соответствует истинному значению параметра.

Для объемных содержаний 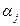справедливо следующее кинематическое соотношение:

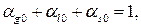(6)

где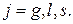

Изменение радиуса пузырька подчиняется уравнению Рэлея-Ламба для пузырька в пористой среде [1].

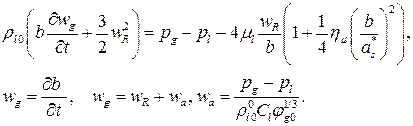(7)

Где 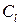– скорость звука в жидкости, 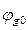– объемная доля газа в пузырьковой жидкости.

Решение системы уравнений будем искать в виде затухающих бегущих волн[1]:

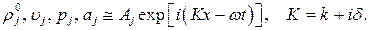(8)

После решения уравнений (1)-(7) получено дисперсионное соотношение [6,7]. Ввиду громоздкости это соотношение не приводится. На основе этого соотношения вычислены фазовая скорость и декремент затухания линейных волн.

⇐ Предыдущая 123 4 5 Следующая ⇒