Линейное уравнение с двумя переменными.

Линейное уравнение с двумя переменными.

Вопросы занятия:

· повторить что такое линейное уравнение с одной переменной и сколько решений может иметь такое уравнение;

· ввести понятия «линейное уравнение с двумя переменными», «решение уравнения с двумя переменными», «равносильные уравнения».

Материал урока

Ранее мы с вами рассматривали линейное уравнение с одной переменной.

Вспомним, что:

Сегодня на уроке мы познакомимся с линейным уравнением, но уже с двумя неизвестными.

Давайте рассмотрим ситуацию

Полученное равенство содержит две переменные. А поэтому такие равенства называют уравнениями с двумя переменными (или с двумя неизвестными).

Посмотрите на примеры уравнений с двумя переменными

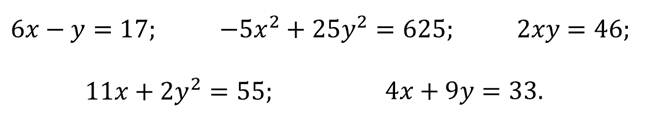
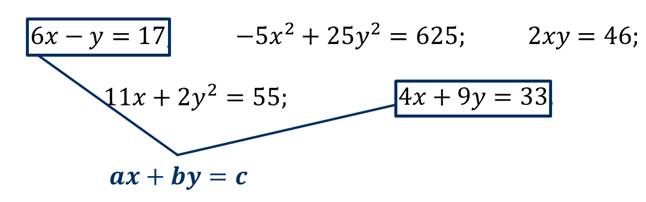
Сформулируем определение:

Определение.

Линейным уравнением с двумя переменными называется уравнение вида:

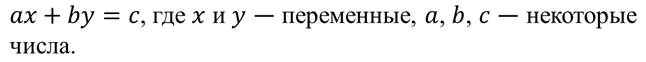
Вернёмся к задаче

То есть пара значений переменных (x = 60, y = 110) является решением этого уравнения. Отметим, что эти корни были найдены методом подбора, причём это не единственная пара чисел, удовлетворяющих нашему уравнению.

Определение.

Решением уравнения с двумя переменными называется пара значений переменных, которая обращает это уравнение в верное равенство.

Вспомним, что при изучении уравнений с одной переменной, мы говорили о равносильных уравнениях, то есть уравнениях, которые имеют одни и те же корни.

Аналогично можем сказать, что уравнения с двумя переменными, имеющие одни и те же решения, называются равносильными.

Причем уравнения с двумя переменными, не имеющие решений, также являются равносильными.

Равносильные уравнения обладают следующими свойствами:

12 Следующая ⇒