
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
ПРОВЕРКА ПРОЙДЕННОГО МАТЕРИАЛА ( компланарность и некомпланарность векторов)
ДИСТАНЦИОННОЕ ОБУЧЕНИЕ
УРОК ЛЕКЦИЯ «Координаты вектора на плоскости и в пространстве»
ПРОВЕРКА ПРОЙДЕННОГО МАТЕРИАЛА ( компланарность и некомпланарность векторов)
Выводы:
1.Любой вектор в пространстве можно разложить по другим векторам( т.е.представить как сумму каких-то векторов), при этом
1 случай: Вектора могут лежать в одной плоскости ( т.е. быть компланарны и не коллинеарны), тогда любой из них можно разложить по другим векторам ( правило сложения векторов)
2 случай : Вектора могут не лежать в одной плоскости ( т.е. быть некомпланарн), тогда их можно разложить по правилу параллелепипеда.)
1. Координаты вектора
Изобразим прямоугольную систему координат Охуz. На каждой из положительных осей от начала координат отложим единичные векторы или координатные вектора , или орты.
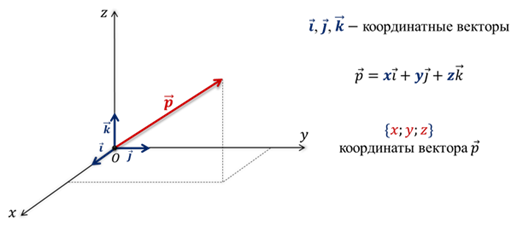
Определение:
Векторы i, j, k будем называть координатными векторами.
Понятно, что они являются некомпланарными. И поэтому любой вектор пространства можно разложить по единичным векторам i, j, k. Причём коэффициенты разложения х, у и z определяются единственным образом.
Коэффициенты х, у и z называют координатами вектора р в данной системе координат. Координаты вектора будем записывать в фигурных скобках в последовательности х, у, z.
Вывод:
Любой вектор в пространстве можно записать 2 способами:
- через его координаты
-через разложение по координатным векторам i, j, k.
.
Закрепление пройденного:
Задание № 1: Пользуясь разложениями векторов по координатным векторам, записать их координаты.
Решение:
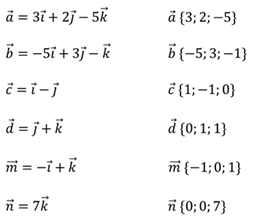
Задание № 2:
Пользуясь координатами векторов, запишем их разложения по координатным векторам i, j, k.
Решение:
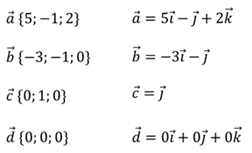
Задача № 3:
В прямоугольном параллелепипеде 𝑂𝐴 = 2, 𝑂𝐵 = 3, а ОО1 = 2. Найти координаты векторов 𝑂𝐴1, 𝑂𝐵1, 𝑂𝑂1, 𝑂𝐶, 𝑂𝐶1, 𝐵𝐶1, 𝐴𝐶1 и 𝑂1 𝐶.
Решение:
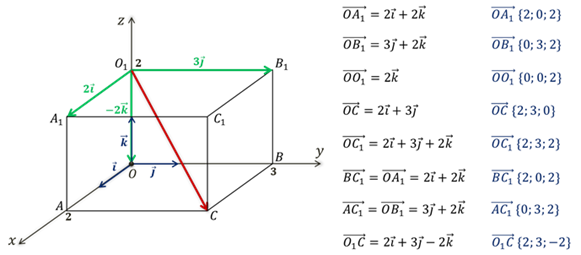
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|