Изучение нового материала.. Теорема. Объём прямой призмы равен произведению площади основания на высоту.. Объем прямого цилиндра пропорционален высоте, т.е. длине его образующей;. Объем прямого цилиндра пропорционален площади его основания.

⇐ ПредыдущаяСтр 2 из 3Следующая ⇒

2. Изучение нового материала.

Теорема. Объём прямой призмы равен произведению площади основания на высоту.

Докажем эту теорему для треугольной призмы, а затем – для произвольной.

Дано: ABCA₁B₁C₁ – прямая призма. Доказать: V = Sосн ·h

А₁ A₁

B₁

C₁

Доказательство.

D₁

Проведем высоту BD_┴АС, которая делит ∆АВС на два прямоугольных треугольника и плоскость (BDD1)_┴(ABC). Получим две призмы, основания которых прямоугольные треугольники, и они прямые, для вычисления объёма применим следствие 2

2) V₁ и V₂их объемы V₁= S_ABD ·h, V₂ = S_DBC ·h,

V= V₁ + V₂ = S_ABD ·h + S_DBC ·h =h · (S_ABD+ S_DBC) = h · S_ABC = Sосн ·h

S₁

S₂

S₃

Рассмотрим n-угольную произвольную призму. Ее можно разбить на (n -2) прямые призмы (рис. 1). Объём каждой треугольной призмы можно вычислить, применяя I часть теоремы

V= V₁+V₂+ V₃+…+ V_n_-2=S₁ ·h +S₂ ·h+S₃ ·h+…+ S_n-2·h = = h · (S₁ + S₂ +S₃+…+S_n-2 )= = Sосн ·h

Таким образом V= Sосн ·h

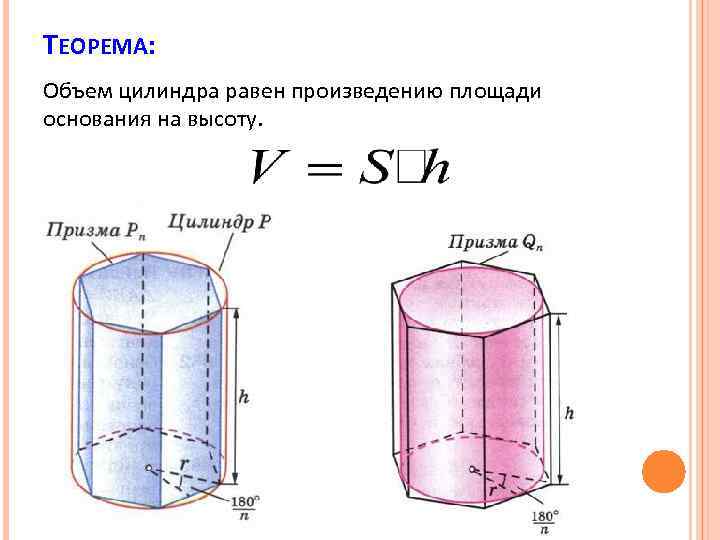
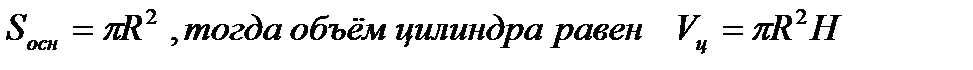
Свойства объема прямого цилиндра:

1. Объем прямого цилиндра пропорционален высоте, т.е. длине его образующей;

Например: объем жидкости в мензурке пропорционален высоте столбика жидкости.

Представим себе прямой цилиндр как бревно постоянного сечения. Будем распиливать его на чурки. Зная длину чурок, мы можем сравнить их объемы. Во сколько раз длиннее чурка во столько же раз будет больше ее объем. Другими словами объем цилиндра пропорционален его высоте.

V₁ = S ∙ h;

V₂ = S ∙ 2h = 2 ∙ Sh;

V₃ = S ∙ 3h = 3 ∙ Sh

2. Объем прямого цилиндра пропорционален площади его основания.

Чтобы убедиться в этом, будем колоть напиленные нами чурки. Раскалывая чурку, мы ударяем по ее верхнему основанию. Какую долю площади основания чурки отколем, такую же долю получим у отколотого полена.

⇐ Предыдущая 123 Следующая ⇒