
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Понятие о производной функции. Правила вычисления производной.
Понятие о производной функции. Правила вычисления производной.
Пусть х0 – произвольная точка в некоторой окрестности фиксированной точки х0. Разность 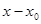 называется приращением независимой переменной (приращением аргумента).
называется приращением независимой переменной (приращением аргумента).
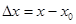 ,
,
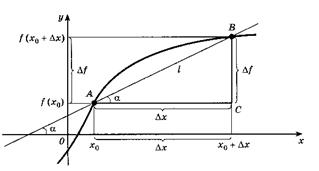 Откуда следует, что
Откуда следует, что 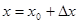 .
.
Первоначальное значение аргумента получило приращение Δх. Вследствие этого значение функции f изменится на величину 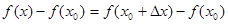 .
.
Эта разность называется приращением функции f в точке х0, соответствующим приращению Δх.
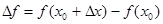 ,
,
Откуда 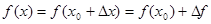 .
.
При фиксированном х0 приращение Δf есть функция от Δх.
Прямую l, проходящую через любые две точки графика функции f, называют секущей к графику f. Угловой коэффициент kсекущей, проходящей через точки А(х0, у0) и В(х; у), равен
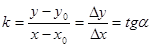 .
.
Производной функции 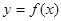 в точке х0 называется число, к которому стремится разностное отношение
в точке х0 называется число, к которому стремится разностное отношение 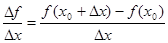 при
при 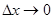 .
.
Таблица производных
Производные функций
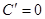 , С – число
, С – число
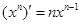
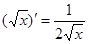
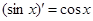
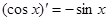
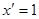
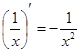
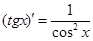
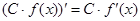
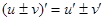
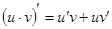
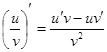
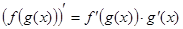
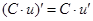
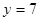 ;
; 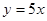 ;
; 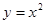 ;
; 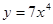 ;
; 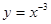 .
.