Решение самостоятельной работы

4. Решение самостоятельной работы

1. В параллелограмме АВСD угол А в 4 раза больше угла D. Найдите угол С.

2. Большее основание равнобедренной трапеции равно13, боковая сторона равна 10. Косинус одного из углов трапеции равен 0,6. Найдите меньшее основание трапеции.

3. Укажите номера истинных утверждений:

1) Диагонали ромба равны.

2) Диагонали прямоугольника равны.

3) Площадь квадрата равна квадрату его стороны.

4) Все углы правильного пятиугольника равны 112°.

5. Решение задач

Задачи по готовым чертежам:

1. Дано: ABCD − ромб.

Найти: MN.

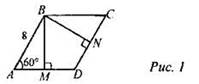
2. Дано: ABCD − параллелограмм.

Найти: ∠CBK.

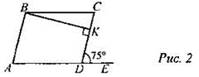
3. Дано: ABCD − ромб.

Найти: АС.

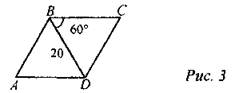
4. Дано: ABCD − ромб,

BE − биссектриса ∠ABD.

Найти: ∠BCD.

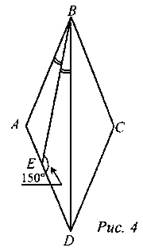
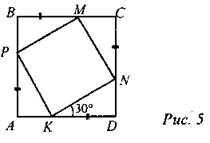
5. Дано: ABCD − квадрат, P_ABCD = 8.

Найти: P_MNKP.

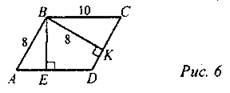
6. Дано: ABCD − параллелограмм.

Найти: BE.

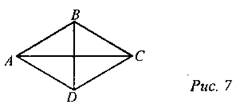
7. Дано: АС = 12, S_ABC_D = 48.

Найти: BD.

8. Дано: ABCD − трапеция.

ВС : AD = 2 : 3,

ВК = 6, S_ABCD = 60.

Найти: ВС, AD.

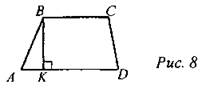
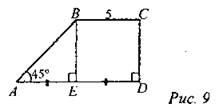
9. Дано: ABCD - трапеция, ВС = 5.

Найти: S_ABCD.

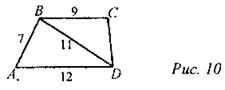
10. Дано: ABCD − трапеция.

Найти: S_ABCD.

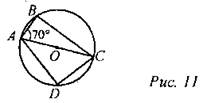
11. Дано: ∪AD = 80°.

Найти: углы четырехугольника ABCD.

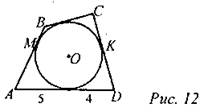
12. Дано: окружность вписана

в четырехугольник ABCD;

М, N, К, Р − точки касания; ВС = 5.

Найти: АВ + CD.

6.Домашнее задание.

1. В равнобокой трапеции боковая сторона равна меньшему основанию, а диагональ перпендикулярна боковой стороне. Найдите углы трапеции.

2. В параллелограмме KMNP угол М равен 120°, КМ = 8, КР = 10. Найдите расстояния от вершин М и Р до биссектрисы угла МКР.

3. Высота ромба делит его сторону пополам. Найдите углы ромба.

4. Внутри квадрата ABCD выбрана точка N так, что треугольник BNC равносторонний. Найдите угол NAD.

5. В параллелограмме ABCD биссектриса угла А пересекает сторону ВС в точке F и продолжение стороны CD за точку С − в точке Е. Найдите периметр параллелограмма, если BF = 2 см, ЕС = 3 см.

⇐ Предыдущая 12