Главная

Контакты

Случайная статья

• Автоматизация
• Антропология
• Археология
• Архитектура
• Биология
• Ботаника
• Бухгалтерия
• Военная наука
• Генетика
• География
• Геология
• Демография
• Деревообработка
• Журналистика
• Зоология
• Изобретательство
• Информатика
• Искусство
• История
• Кинематография
• Компьютеризация
• Косметика
• Кулинария
• Культура
• Лексикология
• Лингвистика
• Литература
• Логика
• Маркетинг
• Математика
• Материаловедение
• Медицина
• Менеджмент
• Металлургия
• Метрология
• Механика
• Музыка
• Науковедение
• Образование
• Охрана Труда
• Педагогика
• Полиграфия
• Политология
• Право
• Предпринимательство
• Приборостроение
• Программирование
• Производство
• Промышленность
• Психология
• Радиосвязь
• Религия
• Риторика
• Социология
• Спорт
• Стандартизация
• Статистика
• Строительство
• Технологии
• Торговля
• Транспорт
• Фармакология
• Физика
• Физиология
• Философия
• Финансы
• Химия
• Хозяйство
• Черчение
• Экология
• Экономика
• Электроника
• Электротехника
• Энергетика

Площадь ромба. Sпараллелограмма = ah, h= Sпараллелограмма: a.

Площадь ромба

Диагонали ромба в точке пересечения делятся пополам, они перпендикулярны и делят ромб на четыре равных прямоугольных треугольника.

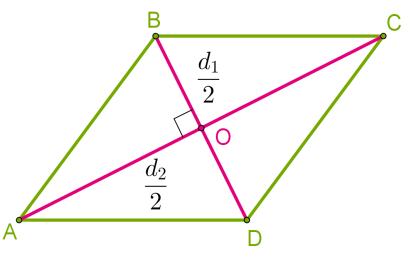
    Формула определения площади ромба:

                                                  Sромба= .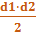

   Эта формула справедлива для определения площади любого четырёхугольника, если его диагонали перпендикулярны.

Так как диагонали квадрата равны, то для определения площади квадрата в формуле достаточно длины одной диагонали: Sквадрата= .

2) Выполните № 697,используя формулу S_{параллелограмма} = ah .

№699. Если вы выполнили задание правильно, то получили 2 группы равновеликих параллелограммов. Параллелограммы равновеликие, если у них одинаковые площади.

(6 кв.ед – а, г, е, ж, з; 8кв.ед.- б, в, д, и).

№701. Решение записать в тетрадь.

Sпараллелограмма = ah, h= Sпараллелограмма: a.

h= 17: 3,4=5(см)

Ответ: h=5см.

№702.

Высота, проведенная между длинными сторонами короче, т.е. 4см.

а= S_{параллелограмма}: h_a =40:4=10(см)

Высота, проведенная между короткими сторонами длиннее, т.е. 5см.

b= S_{параллелограмма}: h_b=40:5=8(см)

Ответ: стороны параллелограмма 10см и 8см.

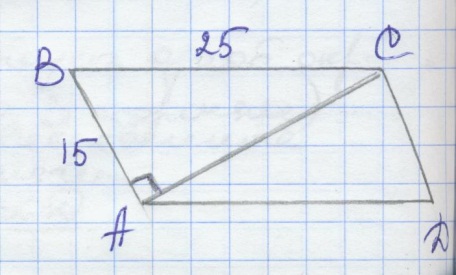№705.

Дано: ABCD – параллелограмм,

AB=12см, BC=25см, AC AB

Найти: S_ABCD-?

Решение:

1)т.к. AC AB, то CAB – прямоугольный. По т.Пифагора AC= 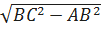= = 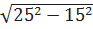= =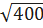20 (см)

2) S_ABCD= AC AB=20 ∙15=300 (см²)

Ответ: S_ABCD=300 см².

Домашнее задание: #21, знать ответы на вопросы, №698(формула+вычисления),№703(с вычислениями).

Скинуть в группу. Проверю выборочно.