Хелпикс

Главная

Контакты

Случайная статья



Тема: «Возрастание и убывание функции» Решение задач.

Стр 1 из 2Следующая ⇒


Тема: «Возрастание и убывание функции» Решение задач.

 

1) Вспомним понятия возрастания, убывания и  монотонности функции  

2) Какими способами нам удавалось определять промежутки монотонности?

1 способ. По определению возрастающей (убывающей) функции.

Рассмотрим пример.  (Слайд 6  и в распечатках)

f(x)= 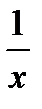, D(f) = (-∞;0)  (0;+∞)

Пусть х2 > x1 , тогда f(x2) - f(x1) = 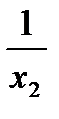-  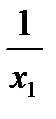= (х1 –х2)/ х2 х1 < 0, значит данная функция убывает на каждом из двух промежутков своей области определения.

2 способ. По графику: готовому либо после его построения.

Пример №2.


      По графику функции y=f(x) ответьте на вопросы:

Сколько промежутков возрастания у этой функции?

Назовите наименьший из промежутков убывания этой функции


 

 

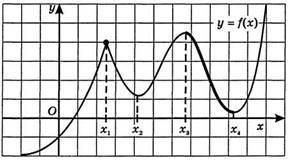
Пример №3


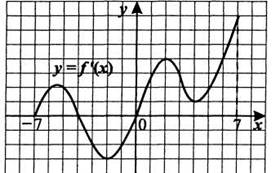
По графику функции y=f ´(x) ответьте на вопросы:

Сколько промежутков возрастания у этой функции?

Найдите длину промежутка убывания этой функции.


 

 

    Функция     Производная Монотонность функции на промежутках, где f/(x) > 0 Монотонность функции на промежутках, где f/(x) < 0
f(x) = x3 – 3x2+ 4      
f(x) = x3 + 3x2- 4      
f(x) = x4 -2x2-3      
f(x) = 2х3 -6х      

Теорема1.

«Если функция f(x) дифференцируема на интервале (a;b)  и  f/(x) >0 для всех х 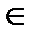(a;b), то функция возрастает на интервале (a;b)».

Теорема2.

«Если функция  f(x) дифференцируема на интервале  (a;b) и f/(x) < 0 для всех х 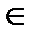(a;b), то функция убывает на интервале (a;b)».

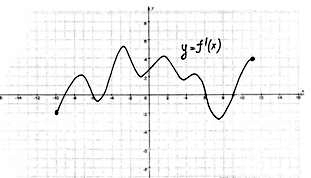
№1. Непрерывная функция y=f(x) задана на [-10;11]. На рисунке изображён график её производной. Укажите количество промежутков возрастания функции.
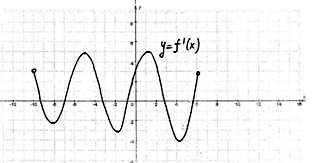
№2. Непрерывная функция y=f(x) задана на (-10;6). На рисунке изображён график её производной. Укажите количество промежутков убывания функции.
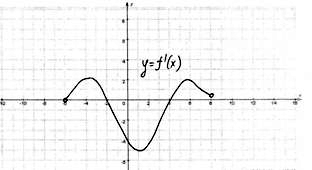
№3. Непрерывная функция y=f(x) задана на (-6;8). На рисунке изображён график её производной. Укажите длину промежутка убывания этой функции.
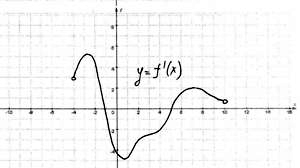
№4. Непрерывная функция y=f(x) задана на (-4;10). На рисунке изображён график её производной. Опишите последовательно типы монотонностей функции.

 

 

По графику функции y=f ´(x) ответьте на вопросы:

Сколько промежутков возрастания у этой функции?

Найдите длину промежутка убывания этой функции.

12Следующая ⇒
  

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.