
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Кроме того, используя функцию распределения можно дать более точное определение НСВ.
Кроме того, используя функцию распределения можно дать более точное определение НСВ.
Определение. Случайную величину X называют непрерывной, если ее функция распределения непрерывна в любой точке.
Приложение 2.
Задача 1.
В партии из 10 изделий имеется 8 стандартных. Наудачу отобраны 2 изделия. а)Составить закон распределения случайной величины Х –числа стандартных изделий среди отобранных.
б) Записать функцию распределения и построить её график.
Решение.
Случайная величина X – число стандартных изделий среди отобранных имеет возможные значения: 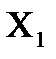 = 0,
= 0, 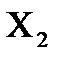 = 1,
= 1, 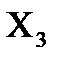 = 2
= 2
Тогда
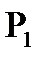 = P(
= P( 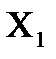 = 1) =
= 1) = 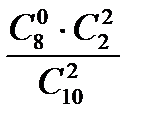 =
= 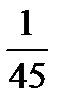
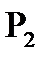 = P(
= P( 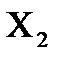 = 1) =
= 1) = 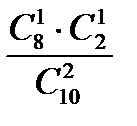 =
= 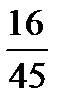
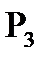 = P(
= P( 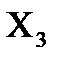 = 2) =
= 2) = 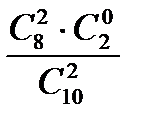 =
= 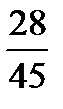
Закон распределения случайной величины Х имеет вид:
| X | |||
| P | 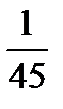
| 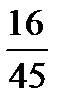
| 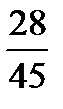
|
Контроль 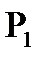 +
+ 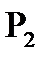 +
+ 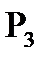 =
= 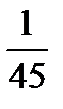 +
+ 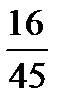 +
+ 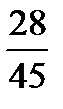 = 1
= 1
Функция распределения имеет вид
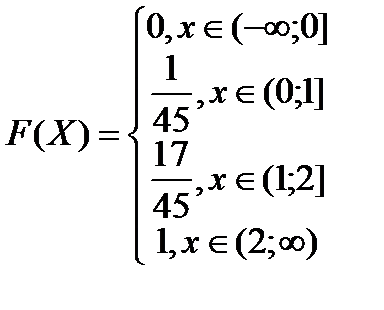
График функции распределения
| F(X) |
| X |
| 0 1 2 |
(на оси ОУ должны быть числа 1/45, 17/45 и 1; на оси ОХ слева до 0 ярче отмечено у=0)
Задача 2
Прибор состоит из четырёх одинаковых узлов, один из которых вышел из строя. Для устранения неисправности случайно выбранный узел заменяется на имеющийся в запасе заведомо исправный и прибор проверяется. Если неисправность не устранена, то один из оставшихся узлов заменяется на исправный, и так до тех пор, пока прибор не заработает.
а) Составить закон распределения случайной величины Х – числа замененных узлов.
б) Записать функцию распределения и построить её график
Решение.
Случайная величина Х – число заменённых узлов – имеет следующие возможные значения: 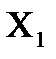 = 1,
= 1, 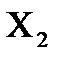 = 2,
= 2, 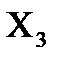 = 3,
= 3, 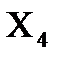 = 4
= 4
Пусть 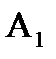 ,
, 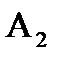 ,
, 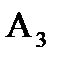 ,
, 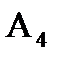 - события, состоящие в том, что неисправный узел обнаружен соответственно с первой, второй, третьей, четвёртой попытки, тогда вероятность возможных значений:
- события, состоящие в том, что неисправный узел обнаружен соответственно с первой, второй, третьей, четвёртой попытки, тогда вероятность возможных значений:
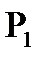 = Р(
= Р( 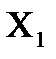 = 1) = P(
= 1) = P( 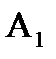 ) =
) = 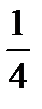
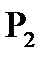 = P(
= P( 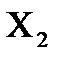 = 2) = P(
= 2) = P( 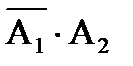 ) =
) = 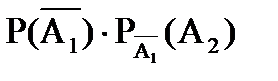 =
= 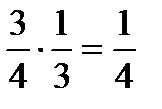
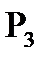 =
= 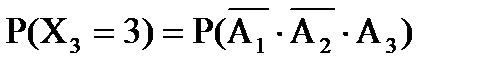 =
= 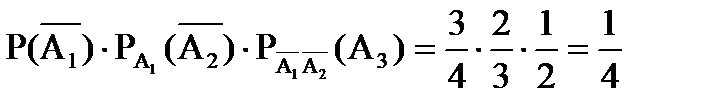
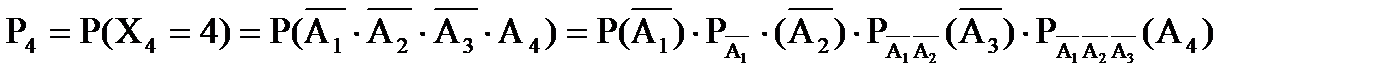 =
=
= 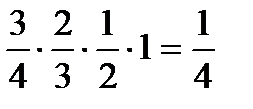
Итак, закон распределения случайной величины Х имеет вид:
| Х | ||||
| Р | 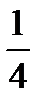
| 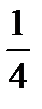
| 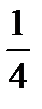
| 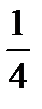
|
Функция распределения случайной величины Х имеет вид:
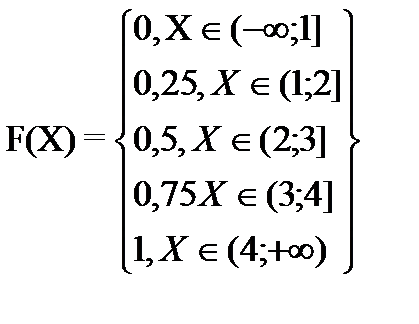
График функции распределения
| F(X) |
| X |
| 1 0,75 0,5 0,25 |
| 2 3 4 |
(на оси ОХ слева до 1должно быть ярче отмечено у=0)
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|