Чтобы не исправлять многократно работы, обязательно прочтите на сайте

Уважаемые студенты,

продолжаем изучать дискретные случайные величины.

Надо разобраться в понятии функции распределения случайной величины (Приложение 1) и выполнить задание на её составление и построение графика.

Примеры решения даны в Приложении 2.

Обращаю внимание на то, что вам не надо составлять закон распределения ДСВ, он уже дан.

Распределение вариантов:

Вариант	Фамилии студентов
	Баталов, Кравцова, Синявская, Рудник, Ошурков, Черноусов, Пономарёв И.,
	Лукина, Изибаев, Саулич, Жигаляк, Трясцин, Касьянов, Никитин, , Отраднов, Третьяков
	Колташев, Пономарев Н., Степанов, Паньшин, Юксеев, Синкин, Чухарев, Перминов
	Игнатов, Нусс, Подрядов, Поросёнков, Армянинова, Генова Колбич, Желудков

Файлы (фото записей в тетрадях) присылать до 12.05 на почту tdpatrakova@mail.ru

Вариант №1 1.Дан закон распределения дискретной случайной величины.

Х
Р	0,1	0,2	0,3	0,2	0,2

Записать функцию распределения и построить её график.

Вариант № 2 1.Дан закон распределения дискретной случайной величины.

Х
Р	0,15	0,2	0,3	0,1	0,25

Записать функцию распределения и построить её график.

Вариант № 3 1.Дан закон распределения дискретной случайной величины.

Х
Р	0,1	0,2	0,5	0,1	0,1

Записать функцию распределения и построить её график.

Вариант № 4 1.Дан закон распределения дискретной случайной величины.

Х
Р	0,2	0,1	0,4	0,2	0,1

Записать функцию распределения и построить её график.

Чтобы не исправлять многократно работы, обязательно прочтите на сайте

http://mathprofi.ru/funkcia_raspredeleniya_dsv.html

способ решения задач с детальным разбором получения функции и особенностей построения графиков.

Приложение 1.

Тема 4. Функция распределения и ее свойства

Универсальным способом задания закона распределения вероятностей, пригодным как для дискретных, так и для непрерывных случайных величин, является функция распределения случайной величины, обозначаемая F(x).

Определение. Функцией распределения случайной величины Х называется функция F(x)=P({X<x}) , выражающая вероятность того, что случайная величина Х примет значение, меньше чем x, где .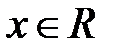

Договоримся писать P(X<x), пропуская фигурные скобки.

Функцию распределения называют еще интегральной функцией распределения.

Функция F(x) обладает следующими свойствами:

1) F(x) ограниченна: 0≤F(x)≤1.

2) F(x) – неубывающая функция, то есть если x₁<x₂, то F(x₁)≤F(x₂).

3) F(x) обращается в ноль на минус бесконечности и равна единице в плюс бесконечности, то есть .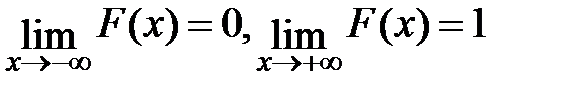

4) Вероятность попадания с.в. X в промежуток [a,b) равна приращению ее функции распределения на этом промежутке, то есть P(a ≤ X ≤ b) = =F(b)-F(a).

5) F(x) непрерывная слева, то есть .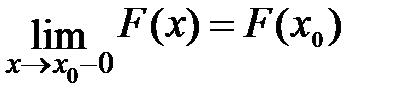

С помощью функции распределения можно вычислить вероятность того, что случайная величина Х примет значение, больше чем x, где 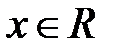: P(X≥x)=1-F(x).

Функция распределения ДСВ X имеет вид 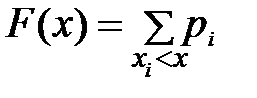(3.5). Здесь суммирование ведется по всем i, для которых x_i<x.

Функция распределения ДСВ X является разрывной функцией со скачками p_i в точках x_i, функцией «непрерывной слева» (при подходе к точке разрыва слева функция сохраняет значение). Ее график имеет ступенчатый вид.

12 Следующая ⇒