
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Формулы приведения.. Формулы приведения. Задачи.
8. Формулы приведения.
Формулы приведения применяются для преобразования выражений вида 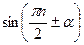 ,
, 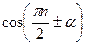 ,
, 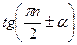 ,
, 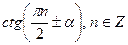 . Для запоминания этих формул используют правило:
. Для запоминания этих формул используют правило:
1) перед приведённой функцией ставится тот же знак, которой имеет исходная функция, если 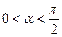 ;
;
2) функция меняется на «кофункцию», если n нечётно; функция не меняется, если n чётно («кофункциями» синуса, косинуса, тангенса и котангенса соответственно являются косинус, синус, котангенс и тангенс).
Значения выражений 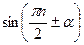 ,
, 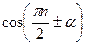 ,
, 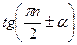 ,
, 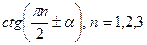 , можно также найти, используя таблицу для формул приведения. Например,
, можно также найти, используя таблицу для формул приведения. Например, 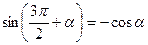 ,
, 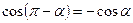 ,
, 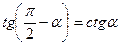 .
.

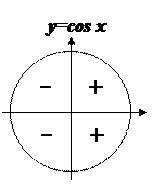
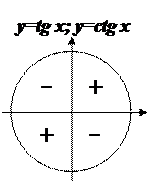
Знаки тригонометрических функций
Формулы приведения
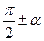
| 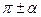
| 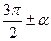
| |
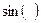
| 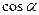
| 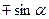
| 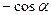
|
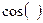
| 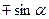
| 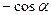
| 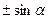
|
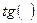
| 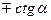
| 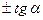
| 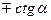
|
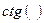
| 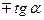
| 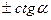
| 
|
Пример 7. Найдите значение выражения 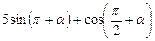 , если
, если 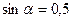 .
.
Решение. Применяем формулы приведения:
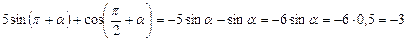
Ответ: -3.
Задачи.
1. Упростите выражение 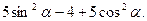
1) 1 2) 9 3)-9 4) -4
2. Упростите выражение 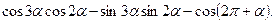
3. Упростите выражение 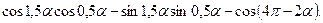
1) 0 2) 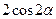 3)
3) 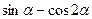 4)
4) 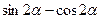
4. Результат упрощения выражения 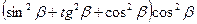 равен
равен
1) 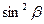 2)
2) 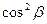 3) 1 4) 2
3) 1 4) 2
5. Результат упрощения выражения 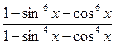 равен
равен
1) 1 2) 1,5 3) 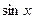 4) -1,5
4) -1,5
5) 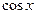 6)
6) 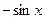 7) -1 8)
7) -1 8) 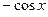
6. Найдите значение выражения 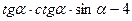 , если
, если 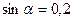 .
.
7. Найдите значение выражения 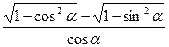 , если
, если 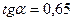 и
и 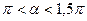 .
.
8.Найдите значение 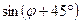 , если
, если 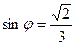 и
и 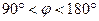 .
.
1) 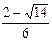 2)
2) 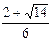 3)
3) 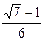 4)
4) 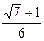
9. Найдите значение 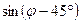 , если
, если 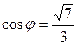 и
и 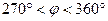 .
.
1) 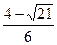 2)
2) 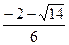 3)
3) 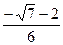 4)
4) 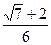
10. Найдите значение выражения 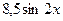 , если
, если 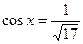 ,
, 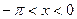 .
.
11. Найдите значение выражения 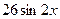 , если
, если 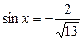 ,
, 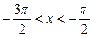 .
.
12. Результат упрощения выражения 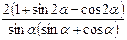 равен
равен
1) 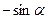 2)
2) 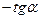 3)
3) 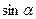 4) 5
4) 5
5) – 8 6) 1 7) -12 8) 4
9) – 1 10) -5 11) 12 12) 8
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|