
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Тема 2. Тождественные преобразования тригонометрических выражений. Тригонометрические функции
Тема 2. Тождественные преобразования тригонометрических выражений. Тригонометрические функции
Задача нахождения синуса, косинуса, тангенса и котангенса произвольного угла сводится к нахождению значений этих функций в случае, когда  . Таблица определяет основные значения
. Таблица определяет основные значения  ,
, 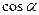 ,
,  и
и  для данного промежутка.
для данного промежутка.
Значения тригонометрических функций основных углов
|
| 
| 
| 
| 
| 
|

| 
| 
| 
| ||

| 
| 
| 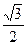
| ||
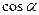
| 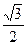
| 
| 
| ||

| 
| 
| - | ||

| - | 
| 
|
Основные тригонометрические формулы
1. Соотношения между тригонометрическими функциями одного и того же аргумента:
1.1.  1.2.
1.2. 
1.3.  1.4.
1.4. 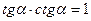
1.5.  1.6.
1.6. 
Пример 1. Найдите значение выражения  , если
, если  .
.
Решение. Применяем основное тригонометрическое тождество (1.1):

Ответ: 4,97.
Пример 2. Найдите значение выражения 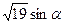 , если
, если  ,
, 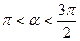 .
.
Решение. Чтобы найти  , используем основное тригонометрическое тождество (1.1) и определяем знак
, используем основное тригонометрическое тождество (1.1) и определяем знак  для значений
для значений 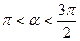 :
:
 ,
,  .
.
Ответ: -4.
2. Формулы сложения:
2.1.  2.2.
2.2. 
2.3.  2.4.
2.4. 
Пример 3. Найдите значение  , если
, если  и
и 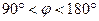 .
.
1)  2)
2) 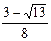 3)
3)  4)
4) 
Решение. Применяем основное тригонометрическое тождество (1.1). Находим  . Выбираем отрицательный знак, так как
. Выбираем отрицательный знак, так как 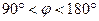 . Тогда по формуле сложения (2.1) получаем:
. Тогда по формуле сложения (2.1) получаем:
 .
.
Ответ: 3).
3. Формулы двойного и тройного аргументов:
3.1. 
3.2. 
3.3. 
3.4. 
3.5. 
4. Формулы преобразования суммы (разности) в произведение:
4.1. 
4.2. 
4.3. 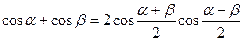
4.4. 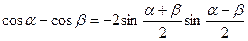
4.5. 
4.6. 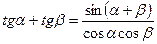 4.7.
4.7. 
Пример 4. Докажите тождество  .
.
Доказательство.
Используем формулы для синуса (3.1) и косинуса (3.2) двойного угла, а также разности синусов (4.2):

 .
.
5. Формулы преобразования произведений в суммы (разности):
5.1. 
5.2. 
5.3. 
6. Формулы понижения степени:
6.1.  6.2.
6.2. 
Пример 5. Выражение  можно преобразовать к виду
можно преобразовать к виду
1)  2)
2)  3)
3)  4)
4) 
Решение. Применяем формулы понижения степени (6.1) и (6.2), а также формулу для синуса двойного угла (3.1):
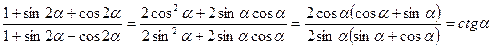 .
.
Ответ: 1).
7. Выражение тригонометрических функций через тангенс половинного аргумента (универсальная подстановка):
7.1.  7.2.
7.2.  7.3.
7.3. 
Пример 6. Вычислите  , если
, если 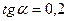 .
.
Решение. Вычислим синус двойного угла с помощью универсальной подстановки (8.1):  . Тогда
. Тогда  .
.
Ответ:  .
.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|
