баллов). КОНУС ( 6 баллов)

(10 баллов)

1. Через образующую цилиндра проведены две такие взаимно перпендикулярные плоскости, что площади полученных сечений равны 3√2 см² каждая. Найдите площадь осевого сечения цилиндра.

2. Диаметр основания конуса 6 см, площадь осевого сечения 12 см². Найдите объем цилиндра, имеющего тот же диаметр основания и одинаковую с конусом величину боковой поверхности.

3. Цилиндр и конус имеют общее основание радиусом 6√3 см. Угол при вершине осевого сечения конуса равен в 120 ⁰. Найдите площадь боковой поверхности цилиндра, если известно, что он имеет равный с конусом объем.

КОНУС ( 6 баллов)

1. Найдите объем конуса, если его осевое сечение равносторонним треугольником со стороной 4 см.

2. Высота и образующая конуса соответственно равны 4 и 5 см. Найдите объем конуса.

3. Найдите объем конуса, с образующей 2√3 м, наклоненной к основанию под углом 30⁰.

4. Найдите площадь боковой поверхности конуса, если его высота равна 3√2 см и составляет с образующей угол 45⁰.

5. Образующая конуса равна периметру прямоугольного треугольника с катетами 3 и 4 см и наклонена к основанию конуса под углом 30⁰. Вычислите объем конуса.

6. Угол между образующей конуса и высотой равен 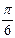. Расстояние от середины образующей до центра основания равно 12 см. Найдите площадь боковой поверхности конуса.

7. Образующая конуса составляет с плоскостью основания угол . Расстояние от центра основания до образующей равно 8 см. Найдите площадь боковой поверхности конуса.

8. Длины двух сторон осевого сечения конуса равны 6 и 12 см. Найдите площадь сечения конуса плоскостью, которая проходит через вершину конуса и хорду основания, стягивающую дугу в 60 ⁰.

9. Один из углов осевого сечения конуса равен 90 ⁰. Хорда основания конуса, которая равна

10. 8√3 см, стягивает дугу в 120 ⁰. Найдите площадь сечения конуса плоскостью, которая проходит через вершину конуса и данную хорду основания.

(10 баллов)

1. Металлический шар радиуса R переплавлен в конус, боковая поверхность которого в два раза больше площади его основания. Найдите высоту конуса.

2. Квадрат боковой поверхности медного конуса вдвое больше квадрата площади основания конуса. Высота конуса равна H. Конус переплавлен в шар. Найдите радикс шара.

3. Осевое сечение конуса представляет собой треугольник с углом α при вершине и радиусом описанной вокруг него окружности R. Найдите объем конуса.

4. Около конуса описана правильная треугольная пирамида, длина каждого ребра которой равно a. Найдите угол при вершине осевого сечения конуса и объем конуса.

5. Около конуса описана правильная четырехугольная пирамида, с длиной каждого ребра a. Найдите угол наклона образующей конуса к плоскости основания и объем конуса.

6. Развертка боковой поверхности конуса – сектор с центральным углом 90 ⁰. Найдите объем конуса, если радиус его основания равен 1 см.

7. Высота конуса равна h, расстояние от центра основания конуса до его образующей равно m. Вычислите через h и m объем конуса (площадь боковой поверхности конуса).

8. Треугольник со сторонами 13,14,15 вращается вокруг средней стороны.Найдите объем тела.

9. Радиус основания конуса равен 1 дм, а угол развертки боковой поверхности равен 90⁰. Вычислить полную поверхность конуса.

10. Образующая конуса равна 6 см, а угол развертки боковой поверхности равен 60⁰. Вычислить объем конуса.

11. Найдите объем конуса, боковая поверхность которого представляет собой круговой сектор с углом 120 ⁰ и радиусом, равным 12 см.

12. Найдите величину угла кругового сектора, представляющего собой развертку боковой поверхности конуса с образующей, равной 8 см, если боковая поверхность конуса в 4 раза больше площади его основания.

13. Развертка боковой поверхности конуса – полукруг. Площадь осевого сечения конуса равна 9√3 см². Найдите объем конуса.

14. Развертка боковой поверхности конуса – сектор с центральным углом 120⁰. Найдите объем конуса, если периметр его осевого сечения равен 16 см.

⇐ Предыдущая 12