Контакты

Случайная статья

Формула Остроградского – Гаусса.

Стр 1 из 2Следующая ⇒

Формула Остроградского – Гаусса.

Связь поверхностного интеграла II рода по замкнутой поверхности S и тройного интеграла по области V ограниченной данной поверхностью устанавливается с помощью формулы Остроградского – Гаусса.

Теорема. Если функции X(x,y,z), Y(x,y,z), Z(x,y,z) непрерывны вместе со своими частными производными первого порядка в некоторой области V, ограниченной поверхностью S, то имеет место формула:

интегрирование по S полагается по внешней стороне.

Доказательство: Пусть область V правильная в направлении оси Oz ограничена:

– снизу поверхностью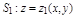

– сверху поверхностью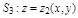

– сбоку цилиндрической поверхностью причем функции и 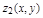непрерывна в области D.

Рассмотрим тройной интеграл

Заменим полученные двойные интегралы поверхностными интегралами II рода по внешней стороне поверхност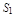и и соответственно.

Добавляя нулевой интеграл по внешней стороне , получим

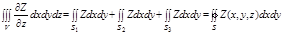
Аналогично выводится и остальные слагаемые формулы Остроградского – Гаусса.

Замечание.

1. Формула Остроградского–Гаусса применяется для вычисления поверхностных интегралов II рода по замкнутой поверхности.

2. Формула Остроградского – Гаусса остается справедливой для любой области V которую можно разбить на конечное число правильных областей.

3. Формула Остроградского – Гаусса применяется для искусственного замыкания поверхности, с целью упрощения процесса интегрирования.

4. Положив в формуле Остроградского – Гаусса.

и подобрав значение для 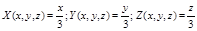при которых данное равенство будет выполняться получим:

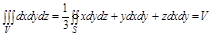
формулу для нахождение объема тела ограниченного снизу поверхностью S₁, сверху поверхностью , а сбоку цилиндрической поверхностью S₂.

Пример. Вычислить 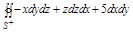, где S: внешняя сторона пирамиды, ограниченной плоскостями .

1.

2.

12 Следующая ⇒

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.