Задача 1.

Задача 1.

Швейной мастерской надо знать, сколько мужских пальто и каких размеров надо сшить. Как это выяснить?

Опросить всех слишком долго и дорого. Поэтому делают выборку: опрашивают выборочно несколько десятков или сотен людей. Допустим, опросили 50 мужчин, их размеры записали в таблицу:

Это – выборка 50 значений (данных). Для удобства её группируют в классы (по размерам) и отмечают, сколько значений выборки содержит каждый класс:

Размер пальто
Количество мужчин

Такие таблицы называются частотными.

По частотной таблице построим гистограмму (столбчатую диаграмму):

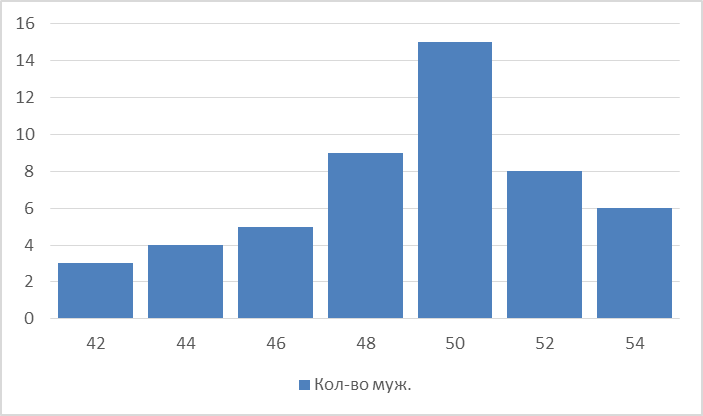
В частотной таблице числа второй строки – частоты; они показывают, как часто встречаются в выборке те или другие её значения. Относительной частотой значения выборки называют отношение его частоты к числу всех значений выборки. В примере частота размера 44 равна 4, а относительная частота 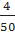= 0,08 = 8%.

Выборки характеризуют центральными тенденциями: средним значением, модой и медианой. Средним значением выборки называют среднее арифметическое всех её значений. Мода выборки– те её значения, которые встречаются чаще всего. Медиана выборки – это число, «разделяющее» пополам упорядоченную совокупность всех значений выборки.

Среднее арифметическоеряда чисел – частное от деления суммы этих чисел на число слагаемых.

Размахряда чисел – разность между наибольшим и наименьшим из этих чисел.

⇐ Предыдущая 123 Следующая ⇒