smax = ± Мх / Wх .

smax = ± Мх / Wх .

Осевые моменты сопротивления стандартных профилей приводятся в справочной литературе. Размерность осевого момента сопротивления – [м³].

Поперечная сила Q_у представляет собой равнодействующую силу внутренних касательных сил – касательных напряжений t, действующих в плоскости сечения. Величина касательных напряжений по высоте поперечного сечения также различна (рис. 5).

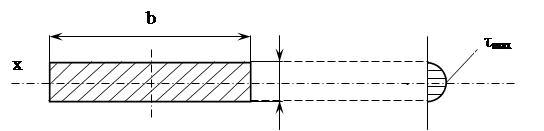Рис. 5. Эпюра касательных напряжений по высоте сечения

Касательные напряжения в произвольной точке поперечного сечения можно вычислить по формуле:

t = (Q_y ∙ S_xω) / (J_x ∙ b_y) ,

где Q_y –поперечная сила в рассматриваемом сечении; S_xω – статический моментотносительно нейтральной оси х той части сечения, которая расположена по одну сторону прямой, проведённой параллельно оси х через данную точку; J_x – момент инерции всего сечения относительно нейтральной оси; b_y – ширина поперечного сечения на уровне рассматриваемой точки.

Для прямоугольного сечения эта формула после подстановки соответствующих величин преобразуется в следующее выражение для определения касательных напряжений:

t = 6 ∙ Q_y ∙ ( h²/4 – y²) / b ∙ h³ .

В точках сечения, наиболее удаленных от нейтральной оси (у = h/2), касательные напряжения равны нулю. Максимальные касательные напряжения действуют в точках нейтрального слоя (у = 0). Они равны :

t_max = 3 ∙ Q_y / (2 ∙ b ∙ h) .

Под действием внешних изгибающих нагрузок ось балки искривляется, поперечные сечения балки перемещаются относительно своих начальных

положений на определенные величины. Эти величины называются прогибами f. Они характеризуют жёсткость балки и являются основной мерой деформации изгиба.

В области упругих деформаций прогибы прямо пропорциональны приложенным нагрузкам: F = k × f . Коэффициент пропорциональности k зависит от схемы нагружения балки, от формы и размеров её поперечных сечений, от материала, из которого она изготовлена, от места расположения рассматриваемого сечения.

В общем случае для определения коэффициентов k, а следовательно и прогибов f , необходимо решать дифференциальные уравнения упругой линии балки. Для наиболее простых случаев нагружения эти уравнения решены и результаты решений приводятся в литературе.

Для случая нагружения, изображённого на рис. 3, максимальным будет прогиб сечения, расположенного в месте приложения силы F. Для данного сечения решение дифференциального уравнения упругой линии балки даёт следующее значение коэффициента пропорциональности:

k = 48 ∙ E ∙ J_x / l³ ,

где Е – модуль упругости материала балки.

Тогда прогиб данного сечения будет равен:

f = F / k = (F ∙ l³) / (48 ∙ E ∙ J_x) .

Коэффициент пропорциональности можно найти экспериментально с помощью лабораторной установки. Для этого необходимо построить зависимость прогибов сечения от нагрузки (рис. 6).

Рис. 6. Зависимость прогибов сечения балки от нагрузки

Коэффициент пропорциональности определяется углом α наклона прямой ОАС :

k = tg α = (F_C – F_A) / (f_C – f_A) .

По результатам испытаний можно определить модуль упругости материала, из которого изготовлена балка:

E = (k ∙ l³) / 48 ∙ J_x .

⇐ Предыдущая 123 Следующая ⇒