Лабораторная работа . ИСПЫТАНИЕ МАТЕРИАЛОВ НА ИЗГИБ .. ОПРЕДЕЛЕНИЕ МОДУЛЯ УПРУГОСТИ МАТЕРИАЛА БАЛКИ

Лабораторная работа

ИСПЫТАНИЕ МАТЕРИАЛОВ НА ИЗГИБ .

ОПРЕДЕЛЕНИЕ МОДУЛЯ УПРУГОСТИ МАТЕРИАЛА БАЛКИ

Цель работы: изучить поведение балки при изгибе; рассчитать напряжения и деформации, возникающие при изгибе балки; определить модуль упругости материала балки.

Теоретическое обоснование

Многие детали и элементы конструкций в процессе эксплуатации испытывают деформацию изгиба. При изгибе происходит искривление оси деформируемого тела. Брусья (стержни), работающие в основном на изгиб, называются балками. Поперечным сечением балки может быть круг, прямоугольник, швеллер, двутавр, уголок, рельс, любая другая более сложная фигура.

В зависимости от условий закрепления различают балки консольные, двухопорные, многоопорные. На рис. 1 изображена двухопорная балка, нагруженная изгибающей силой F. Расстояние l между опорами называется пролетом балки.

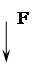Рис. 1. Схема нагружения двухопорной балки изгибающей нагрузкой

Если внешние изгибающие нагрузки действуют в плоскости, проходящей через ось балки, изгиб называют прямым, в противном случае – косым.

Прямым поперечным изгибом называется такой вид деформации балки, когда в её поперечных сечениях возникают два внутренних силовых фактора: изгибающий момент М_х , стремящийся повернуть сечение вокруг его нейтральной оси x , и поперечная сила Q_y, действующая в плоскости сечения и стремящаяся перерезать балку (рис. 2). Если на каком-либо участке балки поперечная сила равна нулю, такой вид напряжённого состояния тела называется чистым изгибом.

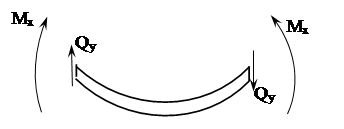Рис. 2. Элемент балки, испытывающий деформацию прямого попереч-

ного изгиба

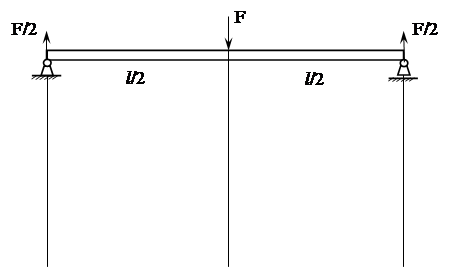
Для наглядного представления о характере изменения поперечной силы и изгибающего момента по длине балки и для нахождения опасных сечений строят эпюры Q_у и M_х (рис. 3).

Рис. 3. Эпюры поперечной силы Q_у и изгибающего момента M_х

Из эпюр можно определить Q_у и M_х в любом поперечном сечении балки. Для данной схемы нагружения наиболее опасным сечением является сечение посередине пролета балки, так как в этом месте действует максимальный изгибающий момент.

Изгибающий момент представляет собой равнодействующий момент внутренних нормальных сил – нормальных напряжений s, действующих в каждой точке поперечного сечения балки и перпендикулярных ему. Значения нормальных напряжений по высоте сечения не одинаковы и изменяются по линейному закону. Нормальное напряжение в любой точке поперечного сечения можно рассчитать по следующей формуле:

s = (М_х/ J_х) × y ,

где М_х – изгибающий момент в данном поперечном сечении; y – расстояние от нейтральной оси х до точки, в которой определяется напряжение; J_х – осевой момент инерции сечения относительно его нейтральной оси х.

Рис. 4. Эпюра нормальных напряжений по высоте сечения

Осевой момент инерции сечения J_хявляется геометрической характеристикой жёсткостипоперечного сечения и зависит только от его формы и размеров. Значения осевых моментов инерции для стандартных профилей приводятся в справочниках, а для простых фигур рассчитываются по формулам. Осевой момент инерции прямоугольного сечения равен:

J_х = b ∙ h³ / 12 ,

где b – сторона сечения, параллельная оси х; h – сторона сечения, перпендикулярная оси х (рис. 4). Размерность осевого момента инерции сечения – [м⁴] .

В точках сечения, лежащих на оси х , нормальные напряжения равны нулю (y = 0). Это значит, что в этом слое балки материал не испытывает ни растяжения, ни сжатия, этот слой называется нейтральным. Линия пересечения нейтрального слоя с плоскостью поперечного сечения балки называется нейтральной осью (линией).

Слои балки, лежащие выше нейтрального слоя, испытывают сжатие, а слои, лежащие ниже его, испытывают растяжение. Максимальные нормальные напряжения возникают в точках, наиболее удаленных от нейтральной оси (y = h/2). Они определяются по формуле:

s_max = ± (М_х/ J_х) × (h / 2) .

В слоях, испытывающих растяжение, напряжения принимают положительными, а в слоях, испытывающих сжатие – отрицательными.

В расчётах на прочность используется такая характеристика поперечного сечения, как осевой момент сопротивления сечения W_x . Он определяется по формуле: W_x = J_x / (h/2). Тогда максимальные нормальные напряжения при изгибе можно рассчитать по формуле:

12 3 Следующая ⇒