Теорема 3. Рекомендованные ссылки на ресурсы сети Интернет

Теорема 3

Если треугольник остроугольный, то высота находится внутри треугольника.

Пусть треугольник остроугольный, но высота – точка 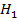, находится вне стороны 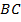(см. рис. 15).

Дано: , , , .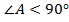

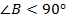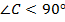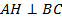Доказать: .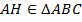

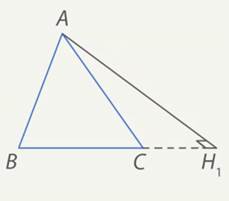
Рис. 15. Иллюстрация к теореме 3

Доказательство: от противного: 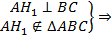противоречие: 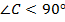(по условию), 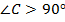( 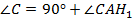) (по теореме о внешнем угле ).

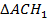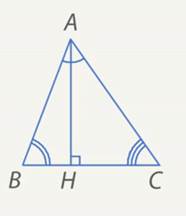
Рис. 16. Доказательство теоремы 3

Итак, высота остроугольного треугольника находится внутри треугольника. Что и требовалось доказать (см. рис. 16).

Рекомендованные ссылки на ресурсы сети Интернет

1. Признаки равенства треугольников (Источник).

2. Первый и второй признаки равенства треугольников. Равнобедренный треугольник (Источник).

3. Свойства треугольника (Источник).