Оценка точности построения аэрофототриангуляции

⇐ ПредыдущаяСтр 55 из 56Следующая ⇒

5.4.Оценка точности построения аэрофототриангуляции

5.4.1.Оценка точности по расхождениям на контрольных точках

В данном примере контрольной была точка 20. Ее точные координаты в метрах следующие:

Х=1604,00; У=804,00; Z=14,00.

Полученные из уравнивания из последнего приближения (рис. 5.72) :

Х=1603,95; У=804,01; Z=14,16

Расхождения координат по модулю составляют соответственно по осям координат: 0,05; 0,01; 0,16.

5.4.2.Оценка точности по значению средней квадратической ошибки единицы веса

Для вычисления средней квадратической ошибки единицы веса найдем значение квадратичной формы .

Выполнив транспонирование вектора поправок V(рис.5.73) и соответствующее умножение (рис.5.74,5.75) находим 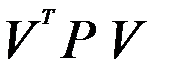=185,966 . Поскольку в нашем примере

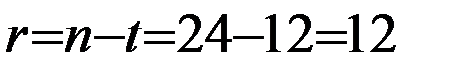то в соответствии с (5.11) найдем(рис.5.76)

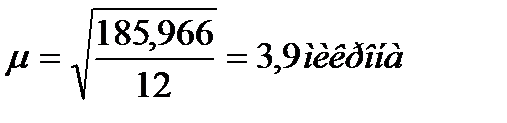
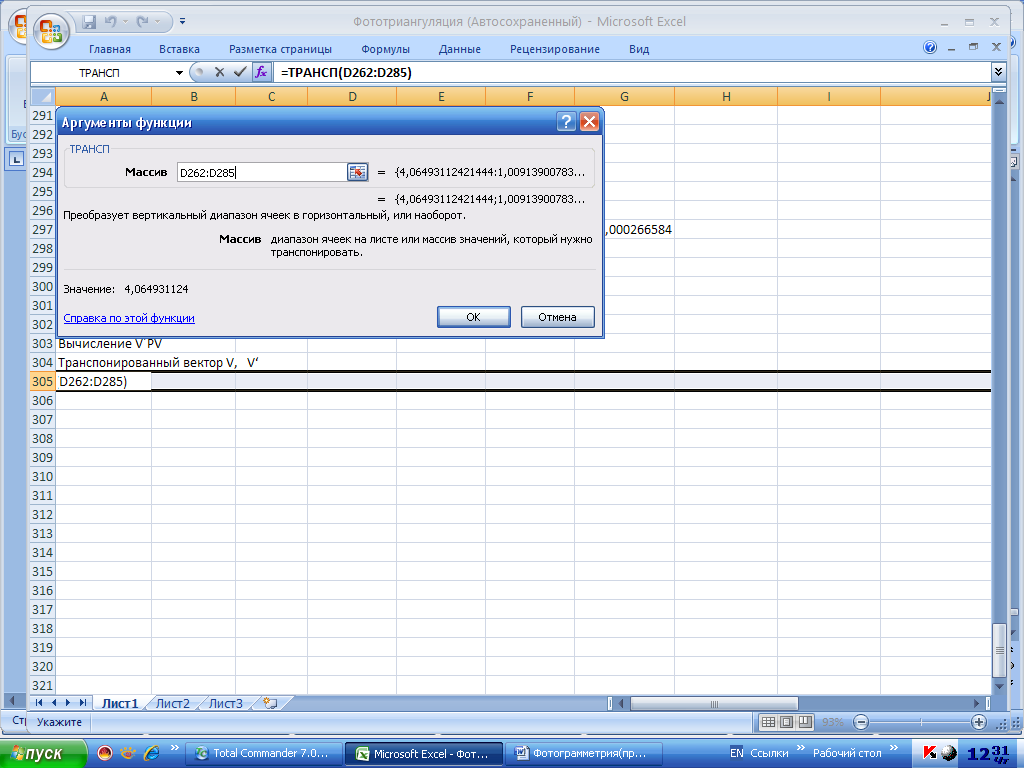
Рис.5.73. Команда транспонирования вектора поправок измерений V

Рис. 5.74. Вычисление

Рис.5.75. Значение

[A4] Рис. 5.76 . Вычисление СКО единицы веса

5.4.3.Оценка точности по средним квадратическим ошибкам уравненных координат определяемых пунктов

Теперь по формуле (5.10) найдем средние квадратические ошибки координат определяемой и контрольной точек. По каждой координате вычисление производится по формуле

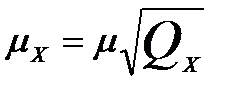, (5.14)

где 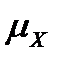- средняя квадратическая ошибка координаты точки, 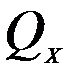- диагональный член обратной матрицы, соответствующий этой координате. В данном примере для координаты Х точки 22 вид соответствующей формулы приведен на рис. 5.77

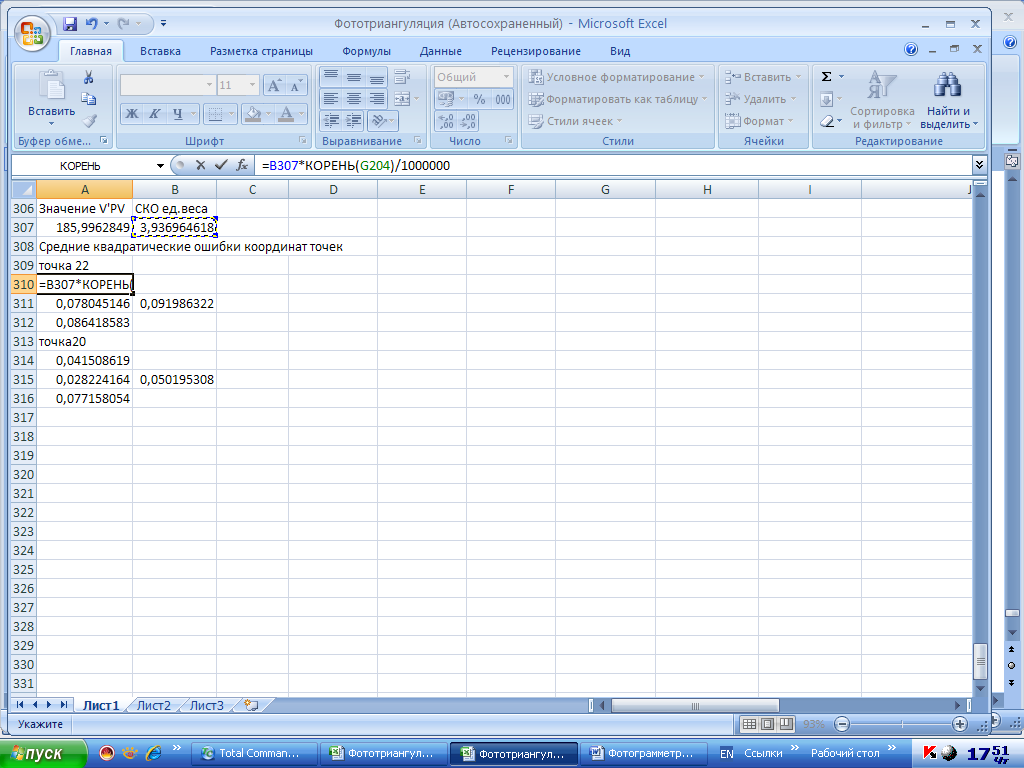
Рис.5.77. Вычисление средней квадратической ошибки точки 22 по оси Х

Здесь G204 – ячейка соответствующего диагонального члена обратной матрицы, КОРЕНЬ( ) – стандартная функция корня, выбранная из категории «Математические»,

1000 000 – множитель перехода от микрон в метры. В307- ячейка СКО единицы веса. На рис. 5.78 приведены средние квадратические ошибки по осям координат обоих точек

Рис. 5.78. Средние квадратические ошибки координат точек.

Средние квадратические ошибки положения точек в плане вычисляются по формуле

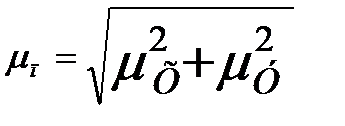где 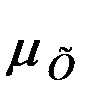, 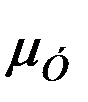- средние квадратические ошибки положения точек по осям Х и У.

Соответствующие вычисления приведены на рис. 5.79

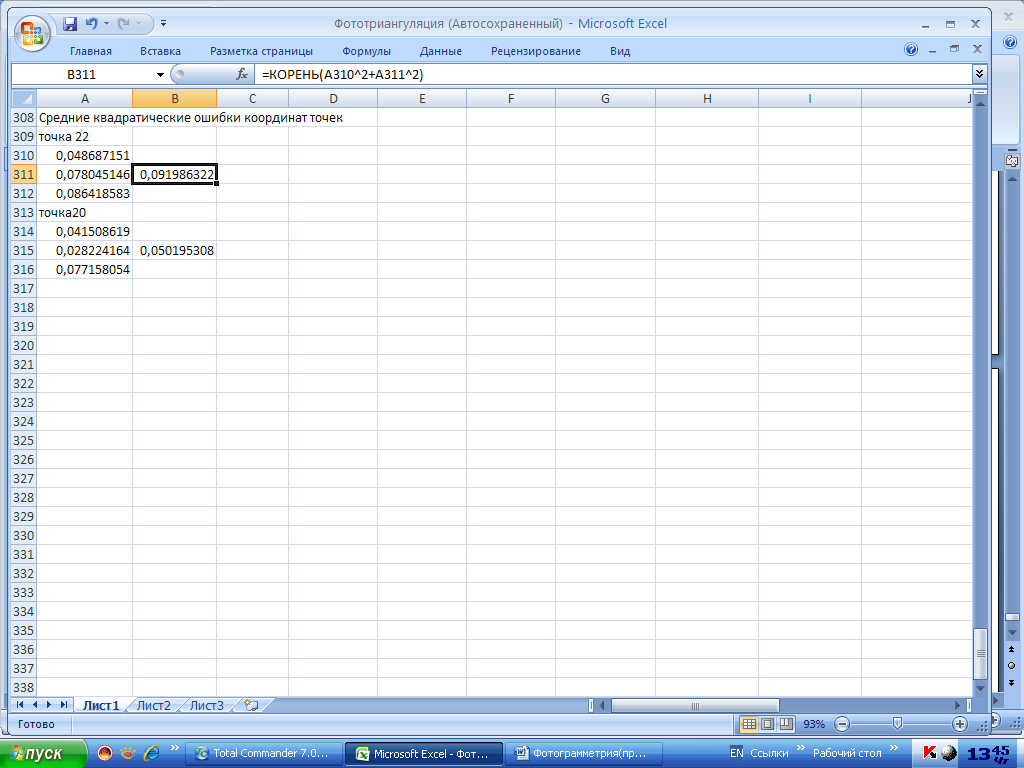
Рис. 5.79. Средние квадратические ошибки планового положения точек

⇐ Предыдущая 47 48 49 50 51 52 53 545556 Следующая ⇒