
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Тема 7. «Тригонометрические уравнения»
Тема 7. «Тригонометрические уравнения»
Задание 1. Уравнение cos x = a
Решить уравнения:

Задание 2. Уравнение sin x = a
Решить уравнения:
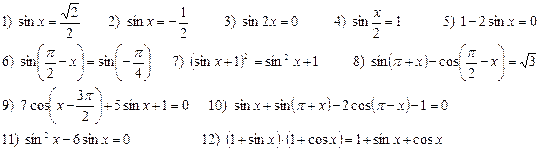
Задание 3. Решение тригонометрических уравнений и неравенств
- Решить уравнения и системы уравнений:
1)  2)
2)  3)
3) 
4)  5)
5)  6)
6) 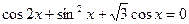 , [ -p, p]
, [ -p, p]
7)  , [ -2p, p] 8)
, [ -2p, p] 8)  , [ 0, 3p]
, [ 0, 3p]
9) 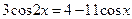 10)
10)  11)*
11)* 
2. Решить систему уравнений:
12)  13)
13)  14)
14) 
15)*  16)*
16)*  17)*
17)* 
3Решить неравенства:
1)  2)
2)  3)
3)  4)
4)  5)
5) 
6)  7)
7)  8)
8)  9)
9)  10)
10) 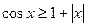
Минимум по теме: задание 1,2( по 5 уравнений), задание 3 (3 системы уравнений и 5 неравенств)
Тема 8. «Координаты и векторы»
Задание 1. Векторы в пространстве
Решение задач по учебнику: «Геометрия 10-11», Л.С.Атанасян и др. № 335, 336, 337, 384
Задание 2. Метод координат в пространстве
Решение задач по учебнику: «Геометрия 10-11», Л.С.Атанасян и др.
№ 402, 403, 404, 407, 410, 426, 429, 431, 444, 451, 501
Минимум по теме: задание 1 (два номера), задание 2 (4 номера)
Тема 9. «Многогранники»
Задание 1. Призма
Задача 1. В прямоугольном параллелепипеде стороны основания равны 12см и 5см. Диагональ параллелепипеда образует с плоскостью основания угол в 450. Найти боковое ребро параллелепипеда.
Задача 2. Основанием прямой призмы является равнобедренная трапеция с основаниями 25см и 9см и высотой 8см. Найти двугранные углы при боковых ребрах призмы.
Задача 3. Через два противолежащих ребра куба проведено сечение, площадь которого равна 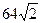 см2. Найти ребро куба и его диагональ.
см2. Найти ребро куба и его диагональ.
Задача 4. Основание прямой призмы – треугольник со сторонами 5см и 3см и углом в 1200 между ними. Наибольшая из площадей боковых граней равна 35см2. Найти площадь полной поверхности призмы.
Задача 5. Боковое ребро наклонной четырехугольной призмы равно 12см, а перпендикулярным сечением является ромб со стороной 5см. Найти площадь боковой поверхности призмы.
Задача 6*. Основание прямой треугольной призмы  - треугольник ABC, в котором
- треугольник ABC, в котором  , а один из углов равен 600. На ребре CC1 отмечена точка P так, что
, а один из углов равен 600. На ребре CC1 отмечена точка P так, что  . Найдите тангенс угла между плоскостями ABC и ABP, если расстояние между прямыми AC и A1B1 равно
. Найдите тангенс угла между плоскостями ABC и ABP, если расстояние между прямыми AC и A1B1 равно  .
.
Задача 7*. В правильной шестиугольной призме  все ребра которой равны 1, найдите угол между прямыми AB1 и BE1 .
все ребра которой равны 1, найдите угол между прямыми AB1 и BE1 .
Задача 8*. В правильной шестиугольной призме  все ребра которой равны 1, найдите косинус угла между прямыми AB1 и BD1 .
все ребра которой равны 1, найдите косинус угла между прямыми AB1 и BD1 .
Примечание: задачи 7 и 8 решаются при помощи векторов (нужно найти угол между векторами)
Задание 2. Пирамида
Задача 1. Основанием пирамиды DABC является треугольник ABC, у которого AB=AC=13см, BC=10см; ребро AD перпендикулярно к плоскости основания и равно 9см. Найти площадь боковой поверхности пирамиды.
Задача 2. Основанием пирамиды является прямоугольник, диагональ которого равна 8см. Плоскости двух боковых граней перпендикулярны к плоскости основания, а две другие боковые грани образуют с основанием углы в 300 и 450. Найти площадь поверхности пирамиды.
Задача 3. Основанием пирамиды DABC является прямоугольный треугольник c гипотенузой BC, BC=10см. Боковые ребра пирамиды равны друг другу, а ее высота 12см. Найти боковое ребро пирамиды.
Задача 4. В правильной треугольной пирамиде SABC M - середина ребра AB, S - вершина. Известно, что BC = 4, SM = 29. Найдите площадь боковой поверхности.
Задача 5. В правильной треугольной пирамиде сторона основания равна 8, а апофема равна  . Найти высоту пирамиды.
. Найти высоту пирамиды.
Задача 6. В правильной четырехугольной пирамиде сторона основания равна 6см, а угол наклона боковой грани к плоскости основания равен 600. Найти боковое ребро пирамиды.
Задача 7. Стороны оснований правильной треугольной усеченной пирамиды равны 4дм и 2дм, а боковое ребро равно 2дм. Найти высоту и апофему пирамиды.
Задача 8.* Ребра AD и BC пирамиды DABC равны 24см и 10см. Расстояние между серединами ребер BD и AC равно 13см. Найдите угол между прямыми AD и BC.
Минимум по теме: задание 1 (три задачи), задание 2 (три задачи).
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|