
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Тригонометрия. Тема 5. «Тригонометрические функции». Задание 1. Число на единичной окружности. Тема 6. «Тригонометрические формулы». Тождественные преобразования тригонометрических выражений
2 СЕМЕСТР
Тригонометрия
Тема 5. «Тригонометрические функции»
Задание 1. Число на единичной окружности
Описать все числа x, для которых (решить графически уравнения и неравенства):
А) 
Б) на отрезке  :
: 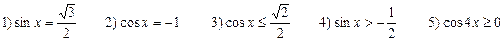
Задание 2. Функция 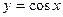
1) По графику функции 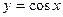 :
:
1.1) Определить, сколько корней имеет уравнение: 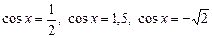
1.2) Определить, сколько корней на отрезке  имеет уравнение:
имеет уравнение: 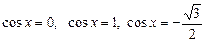
1.3) Найти корни уравнения 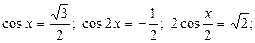
2) Найти множество значений функции: 
3) Построить график функции: 
4) Найти область определения функции 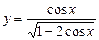 ;
; 
Задание 3. Функция 
1) По графику функции  :
:
1.1) Определить, сколько корней имеет уравнение: 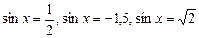
1.2) Определить, сколько корней на отрезке  имеет уравнение:
имеет уравнение:
. 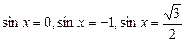
1.3) Найти корни уравнения 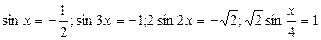
2) Найти множество значений функции: 
3) Построить график функции: 
4) Найти область определения функции 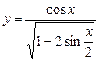
5) *Исследовать функцию 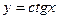 и построить ее график
и построить ее график
Минимум по теме: задания 2 и 3 (в каждом задания 1, 2)
Тема 6. «Тригонометрические формулы»
Тождественные преобразования тригонометрических выражений
1) Найти: 2) Упростить:
а) cos x, если sin x = 12/13, p/2 < x <p а) cos(2p-3x) cos x + sin3x cos(3p/2 + x)
б) sin x, если cos x = -15/17, p < x < 3p/2 б) sin(p-3x) cos x + cos3x cos(3p/2 - x)
в) tg x, если cos x = 2/5, 0 < x < p/2) в) 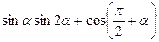
г) cos x, если ctg x = -Ö2, p/2 < x < p г) 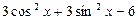
д) 
3) Найти значение выражения: а) sin(p/2 + a) – 4cos(p-a), если cosa = -0,4
б) 
4) Вычислить: а) 
5) Доказать тождества: 5.1)  5.2)
5.2) 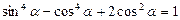
5.3) 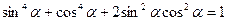 5.4)
5.4) 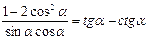
Минимум по теме: 1 а), б); 2 а), б), в); 3 а); 4 а); 5 (2 тождества)
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|