
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Таким образом, получаем, что
α β γ δ ε ζ η θ ι κ λ μ ν ξ ο π ρ ς σ τ υ φ χ ψ ω
Замечания к выполнению расчетно - графической работы по теории вероятностей(2 курс)
Замечание 1:
Если случайная величина (с.в.) 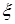 имеет равномерное распределение на отрезке
имеет равномерное распределение на отрезке 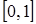 , то с.в.
, то с.в. 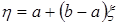 имеет равномерное распределение на отрезке
имеет равномерное распределение на отрезке 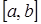 .
.
Замечание 2:
С.в. 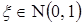 , где символ
, где символ 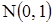 обозначает, что с.в.
обозначает, что с.в. 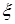 имеет стандартное нормальное распределение, может быть удовлетворительно представлена случайной величиной
имеет стандартное нормальное распределение, может быть удовлетворительно представлена случайной величиной 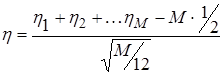 , где
, где 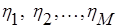 - независимые одинаково распределенные случайные величины (н.о.р.с.в.). Причем с.в.
- независимые одинаково распределенные случайные величины (н.о.р.с.в.). Причем с.в. 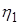 имеет равномерное распределение на отрезке
имеет равномерное распределение на отрезке 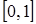 . Для хорошей аппроксимации рекомендуется брать
. Для хорошей аппроксимации рекомендуется брать 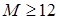 .
.
Замечание 3:
Пусть 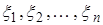 - н.о.р.с.в. и
- н.о.р.с.в. и 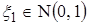 .
.
Тогда с.в. 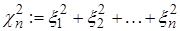 имеет
имеет 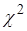 (хи - квадрат) - распределение с n степенями свободы.
(хи - квадрат) - распределение с n степенями свободы.
Замечание 4:
Пусть 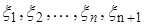 - н.о.р.с.в. и
- н.о.р.с.в. и 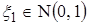 .
.
Тогда с.в. 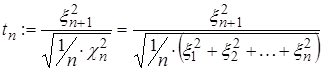 имеет t распределение Стьюдента с N степенями свободы.
имеет t распределение Стьюдента с N степенями свободы.
Замечание 5:
Пусть 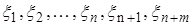 - н.о.р.с.в. и
- н.о.р.с.в. и 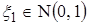 .
.
Тогда с.в. 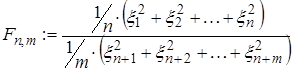 имеет F распределение Фишера с n и m степенями свободы.
имеет F распределение Фишера с n и m степенями свободы.
Замечание 6:
Пусть 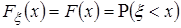 - есть строго непрерывная и возрастающая функция распределения с.в.
- есть строго непрерывная и возрастающая функция распределения с.в. 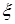 .
.
Тогда с.в. 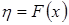 имеет равномерное распределение на отрезке
имеет равномерное распределение на отрезке 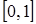 . Отсюда следует, что если с.в.
. Отсюда следует, что если с.в. 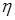 имеет равномерное распределение на отрезке
имеет равномерное распределение на отрезке 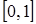 , а функция
, а функция 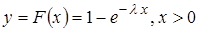 есть функция распределения показательного закона с параметром
есть функция распределения показательного закона с параметром 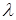 , то с.в.
, то с.в. 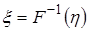 имеет показательное распределение с параметром
имеет показательное распределение с параметром 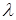 . Здесь
. Здесь 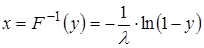 - есть обратная функция для
- есть обратная функция для 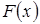 .
.
Замечание 7:
Пусть 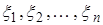 - н.о.р.с.в. и
- н.о.р.с.в. и 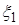 имеет показательное распределение с параметром
имеет показательное распределение с параметром 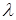 . Плотность такого распределения имеет вид:
. Плотность такого распределения имеет вид:
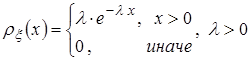
Тогда с.в. 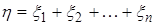 - имеет гамма распределениес параметрами
- имеет гамма распределениес параметрами 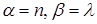 . В дальнейшем для обозначения гамма распределения будем использовать символ
. В дальнейшем для обозначения гамма распределения будем использовать символ 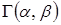 .
.
Плотность гамма распределения имеет вид:
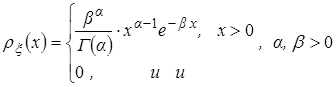 ,
,
где 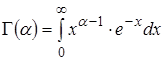 - гамма функция Эйлера.
- гамма функция Эйлера.
Гамма функция обладает следующими свойствами:
1. 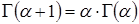 ;
;
2. 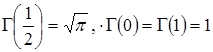 ;
;
3. 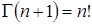 , где n – натуральное.
, где n – натуральное.
Показательное распределение является частным случаем гамма распределения с параметрами 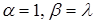 !!!
!!!
Замечание 7:
Пусть n – натуральное число, с.в. 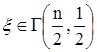 , т.е. имеет гамма распределение с параметрам
, т.е. имеет гамма распределение с параметрам 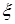 и
и 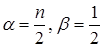 . Тогда с.в.
. Тогда с.в. 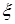 имеет
имеет 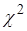 (хи - квадрат) - распределение с n степенями свободы.
(хи - квадрат) - распределение с n степенями свободы.
Т.о. 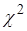 - распределение также является частным случаем гамма распределения!!!
- распределение также является частным случаем гамма распределения!!!
Замечание 8:
Пусть мы рассматриваем некоторую с.в. 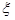 . Будем k раз ее измерять (в одинаковых условиях, независимо друг от друга).
. Будем k раз ее измерять (в одинаковых условиях, независимо друг от друга).
Рассмотрим последовательность н.о.р.с.в. 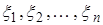 , таких, что
, таких, что
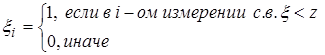
z – некоторое фиксированное число.
Обозначим через 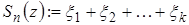 - число измерений с.в.
- число измерений с.в. 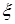 меньших z.
меньших z.
Тогда с.в. 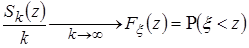 (в некотором смысле сходится к функции распределения).
(в некотором смысле сходится к функции распределения).
Тогда если 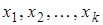 - наблюдаемые значения с.в.
- наблюдаемые значения с.в. 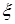 , то в качестве оценки значения функции
, то в качестве оценки значения функции 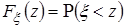 в точке z можно использовать наблюдаемые значения
в точке z можно использовать наблюдаемые значения 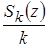 , вычисленные по наблюдениям
, вычисленные по наблюдениям 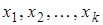 .
.
Замечание 9*:
Пусть с.в. 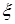 имеет абсолютно непрерывное распределение. Квантилью порядка p
имеет абсолютно непрерывное распределение. Квантилью порядка p 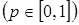 с.в.
с.в. 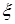 называется число
называется число 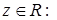
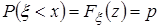 .
.
Замечание 10:
Пусть необходимо вычислить значение 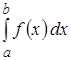 . Введем в рассмотрение с.в.
. Введем в рассмотрение с.в. 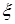 , имеющую равномерное распределение на
, имеющую равномерное распределение на 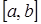 и с.в.
и с.в. 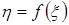 .
.
Вычислим математическое ожидание 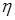 :
:
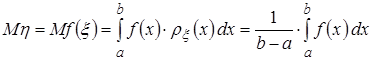 .
.
Таким образом, получаем, что
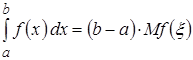 , где
, где 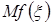 - есть математическое ожидание с.в.
- есть математическое ожидание с.в. 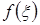 .
.
Пусть 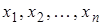 - полученные (“наблюденные”) значения с.в.
- полученные (“наблюденные”) значения с.в. 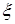 (наблюдения произведены в неизменных условиях, независимо друг от друга), тогда величины
(наблюдения произведены в неизменных условиях, независимо друг от друга), тогда величины 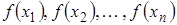 можно рассматривать как значения с.в.
можно рассматривать как значения с.в. 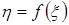 .
.
Отсюда следует, что 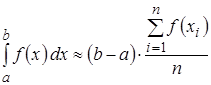 . Величина
. Величина 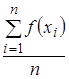 является “хорошей” (некотором смысле) оценкой (аппроксимацией)
является “хорошей” (некотором смысле) оценкой (аппроксимацией) 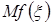 .
.
Замечание 11:
Пусть необходимо найти площадь некоторой области D.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|