Снежинка Коха

Снежинка Коха

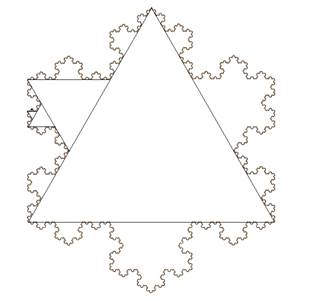
Из геометрических фракталов очень интересным и довольно знаменитым является фрактал "Снежинка Коха". Строится она на основе равностороннего треугольника.
Пусть сторона исходного треугольника равна 1. Его площадь также равна 1.

Каждая сторона делится на три части каждая длиной в 1/3 исходной стороны. Затем пририсовываются три меньших равносторонних треугольника по одному на каждой стороне (на средней трети). На каждой из полученных 12 сторон пририсовываются по одному ещё меньшему треугольнику (снова на средней трети стороны).

Таким образом, с каждой итерацией длина кривой увеличивается на треть.

Этот процесс можно продолжать бесконечно долго.

Каждый раз число сторон учетверяется. Число сторон можно выразить такой последовательностью:

3, 3*4, 3*4*4, 3* 4*4*4, 3* 4*4*4*4....

Убеждаемся, что число сторон снежинки бесконечно велико.

Снежинка образуется добавлением треугольника к каждой стороне, так что выписанная последовательность даёт также и число треугольников, добавляемое на каждом этапе (каждой итерации). Начиная со второго этапа, количество добавляемых треугольников каждый раз учетверяется.

В математике , А иерархия является теоретико-множеством объектов, состоящая из предпорядка , определенный на множестве. Это часто упоминается как упорядоченное множество , хотя это неоднозначный термин , который многие авторы резерв частично упорядоченных множеств или упорядоченных множеств . Термин предварительно упорядоченное множество является однозначным, и всегда синоним математической иерархии. Термин иерархия используется , чтобы подчеркнуть в иерархическое соотношение между элементами.

Математическая иерархия (предварительно упорядоченное множество) не следует путать с более общим понятием иерархии в социальной сфере, в частности , когда один строит вычислительные модели , которые используются для описания реальных социальных, экономических или политических систем. Эти иерархии, или сложные сети , являются слишком богаты , чтобы быть описаны в категории Набор множеств. Это не просто педантичный требование; Есть также математические иерархии, не описываемые с помощью теории множеств.

Еще одна естественная иерархия возникает в информатике , где слово относится к частично упорядоченные множества , элементы которых классы объектов возрастающей сложности . В этом случае предпорядок определения иерархии является класс сдерживания отношения. Сдерживание иерархии , таким образом , особые случаи иерархий.

Общее между фрактальность и иерархичность:

1. Вычислительные модели

2. Графические

3. Геометрических

Разница

1. Иерархия структура с вертикальной формой управления контроля элементами входящ0ие в нее

2. фрактальность множество , обладающей само подобие

⇐ Предыдущая 123 Следующая ⇒