МЕТОДЫ СИНТЕЗА ОБЪЕКТОВ В САПР.

7.МЕТОДЫ СИНТЕЗА ОБЪЕКТОВ В САПР.

1. Перебор законченных структур для объектов 1 и 2 уровней сложности – сравниваются различные структуры объекта с заданными параметрами и выбираются наилучшее с точки зрения критерия оптимизации.

2. Перебор законченных структур для задач 3 и 4 уровня сложности – когда полный перебор невозможен, пользователь задает структуру, программа оценивает ее оптимальность, решая задачи дискретного математического программирования. Пример: необходимо найти экстремумы для функции когда х ? хD, где х -независимая переменная, хD –область допустимых значений независимой переменной. Оптимальное значение х находится в пределах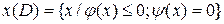

φ(х),ψ(х) –ограничения на независимые переменные. Примером задачи программирования является выбор оборудования.

3. Наращивание структуры к начальному элементу поэтапно добавляются последующие элементы. На каждом этапе происходит проверка критерия оптимальности. Пример: разводка печатной платы.

4. Выделение варианта из обобщенной структуры – если известно описание более широкого класса объектов, то из него всегда можно выделить описание, которое относится к более узкому классу объекта. Пример: определение маршрута изготовления деталей из общей технологии изготовления изделия.

5. Трансформация описания - переход от описания объекта выполненного на одном уровне иерархии или одним способом к описанию выполненному на другом уровне иерархии или другим способом.

В трансформации описаний используются для синтеза проектных решений и для верификации проектных решений.

8. МОДЕЛИРОВАНИЕ ОБЪЕКТА ПРОЕКТИРОВАНИЯ С ПОМОЩЬЮ СЕТЕЙ ПЕТРИ.

На системном уровне моделирования ведется с помощью систем массового обслуживания (СМО) или сетей Петри. Сеть Петри служит для моделирования дискретных асинхронных объектов при этом применяется допущения, что все события происходят разновременно и мгновенно. Сеть Петри определяется множеством: S = <P,T,I,O>

Р- подмножество определяющее условие( обозначается О);

Т- подмножество переходов, определяют события (обозначается );

I –множество входных дуг, дуга соединяющая позиции с переходами;

О –множество выходных дуг, соединяющие переходы с позициями.

С помощью сетей Петри моделируются процессы, представленные в виде последовательности событий. Каждому из возможных событий соответствует определенный переход.

Каждое событие происходит, если выполнено условие. Выполнение условий отображается маркерами, помещаемыми в виде точек внутри соответствующих позиций. Моделирование событий сетями Петри выражается в перемещении маркеров м/д позициями.

Пример работы сети Пери при моделировании простой вычислительной системы. Моделируется поступление задачи на вход решения и ее выход из системы.

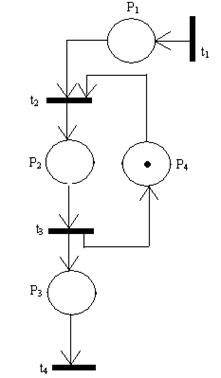Позиция Р1 - определяет наличие задачи на входе вычислительной системы; Р2 – процессор занятия решением задачи; Р3 –на выходе системы есть решенная задача; Р4 –процессор свободен.

t1 –переход, определяет событие: на вход системы поступает задача; t2 –начало решения задачи; t3 – задача решена; t4 –передача задачи на выходе системы.

Для определения состояния системы в каждый момент времени составляется матрица состояния системы. По столбцам отражаются позиции по строкам дискретные моменты времени.

В момент времени Т1 появляется задача. В момент Т2 задача поступает во входную очередь в Т3. Т4 –задача решена процессор освобождается и а выходе результат.

Разновидности сетей Петри.

Временная сеть Петри. Вводятся задержки при перемещение маркеров. Задержки могут быть детерминированными и случайными величинами. Разновидность - стохастическая сеть Петри, со случайными задержками. Возможно введение вероятности срабатывания перехода для разрешения конфликтной ситуации

Цветная сеть Петри. Маркеры отличаются друг от друга по цвету, маркеры разного цвета запускают разные переходы.

Ингибиторные сети содержат запрещающие ( ингибиторные) ветви, в которой при наличии маркера во входной позиции запрещен запуск перехода.

Автоматная сеть - каждый переход имеет один вход и один выход (число маркеров постоянное)

⇐ Предыдущая 1 2 34