ЗАДАЧА РАССЛОЕНИЯ МПП

ЗАДАЧА РАССЛОЕНИЯ МПП

Для системы проводников составляется граф пересечений вершина которого соответствует проводникам, а ребра их пересечениям.

Хроматическим числом графа называется наименьшее кол-во

цветов с помощью которых можно раскрасить его вершины

так, чтобы в нем не было ни одного ребра соединяющего

вершину одного цвета.

Число слоев МПП равно хроматическому числу графа

Результат расслоения проводников

В одном слое размещаются только проводники одного цвета

5-6. МЕТОДЫ АНАЛИЗА МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ.

Анализ математических моделей разделяется на одновариантный и многовариантный.

Одновариантный анализ. Большинство задач одновариантного анализа сводится к решению систем линейных алгебраических уравнений вида АХ=В, где А - матрица (nхn) с большим количеством нулевых элементов, Х- n- мерный вектор неизвестных, В- n- мерный заданный вектор. Численные методы решения разделяются на итерационные и прямые. Итерационные методы просты в реализации и требуют минимальных затрат оперативной памяти. Прямые методы основаны на применении методов Гаусса. Для решения нелинейных алгебраических уравнений применяется метод Ньютона, метод деления отрезка пополам.

Многовариантный анализ – используется для верификации проектного решения.

Методы решения: анализ чувствительности, метод наихудшего случая, метод Монте–Карло.

Анализ чувствительности: определяется коэффициент чувствительности выходных параметров (J) к изменению внутренних (X) или внешних Q параметров.

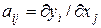
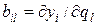
При анализе чувствительности составляется матрица коэф. чувствительности, где отражаются все внутренние параметры влияющие на выходные параметры.

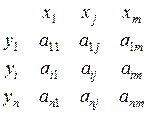(1)

Матрицы чувствительности А и В размером nxm (1) состоят из значений аij для n выходных, m внутренних, l внешних параметров. В САПР аналитических выражений связывающих входные, внутренние и выходные переменные нет. Поэтому коэф. определить прямым дифференцированием не возможно, поэтому от частных производных переходят к приращениям, т.е. задается малое приращение внутреннего или внешнего параметра и определяется изменение выходного параметра. Это значит, что проводится (m+1) раз одновариантный анализ.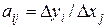

Метод Монте-Карло основан на многократном моделирование числовых значений вектора % внутренних параметров и расчета для каждого сочетания выходных параметров У. Алгоритм метода Монте-Карло. 1.Случайным образом задается вектор Х внутренних параметров с определенными отклонениями. Вектор не коррелирован, т.е. нет связей м/д отдельными параметрами. 2.Проводится корреляция вектора внутренних параметров, т.е. корректируются значения элементов вектора в соответствии с коэф. корреляции получаем вектор хl.

Метод наихудшего случая. Относится к статическим методам. Для его реализации необходимы начальные входные данные: максимально возможные отклонения ∆qi элементов вектора внешних параметров от номинальных; закон распределения внутренних параметров; техническое требование на выходные параметры yi. Задача анализа в нахождении знака коэф. чувствительности и максимального отклонения входного параметра. Определяется область работоспособности и если изделие работоспособно в условиях наихудшего случая, то оно работоспособно во всем пространстве внешних параметров. (1-граница работоспособности, 2 -область работоспособности)

3Проводится одновариантный анализ(расчет выходных параметров).

4. Проводится анализ результатов моделирования.

5. Повторяются шаги 1-4 заданное количество раз.

6. Проводится анализ результатов, т.е. определяется вероятности работоспособности объекта для заданного количества испытаний. Чем больше проведено вариантов внутренних параметров, тем выше вероятность работоспособности объекта при заданных значениях внутренних параметров, тем больше времени требуется на реализацию метода.

⇐ Предыдущая 1 234 Следующая ⇒