Тема: «Примеры функциональных зависимостей в реальных процессах и явлениях.»

Тема: «Примеры функциональных зависимостей в реальных процессах и явлениях.»

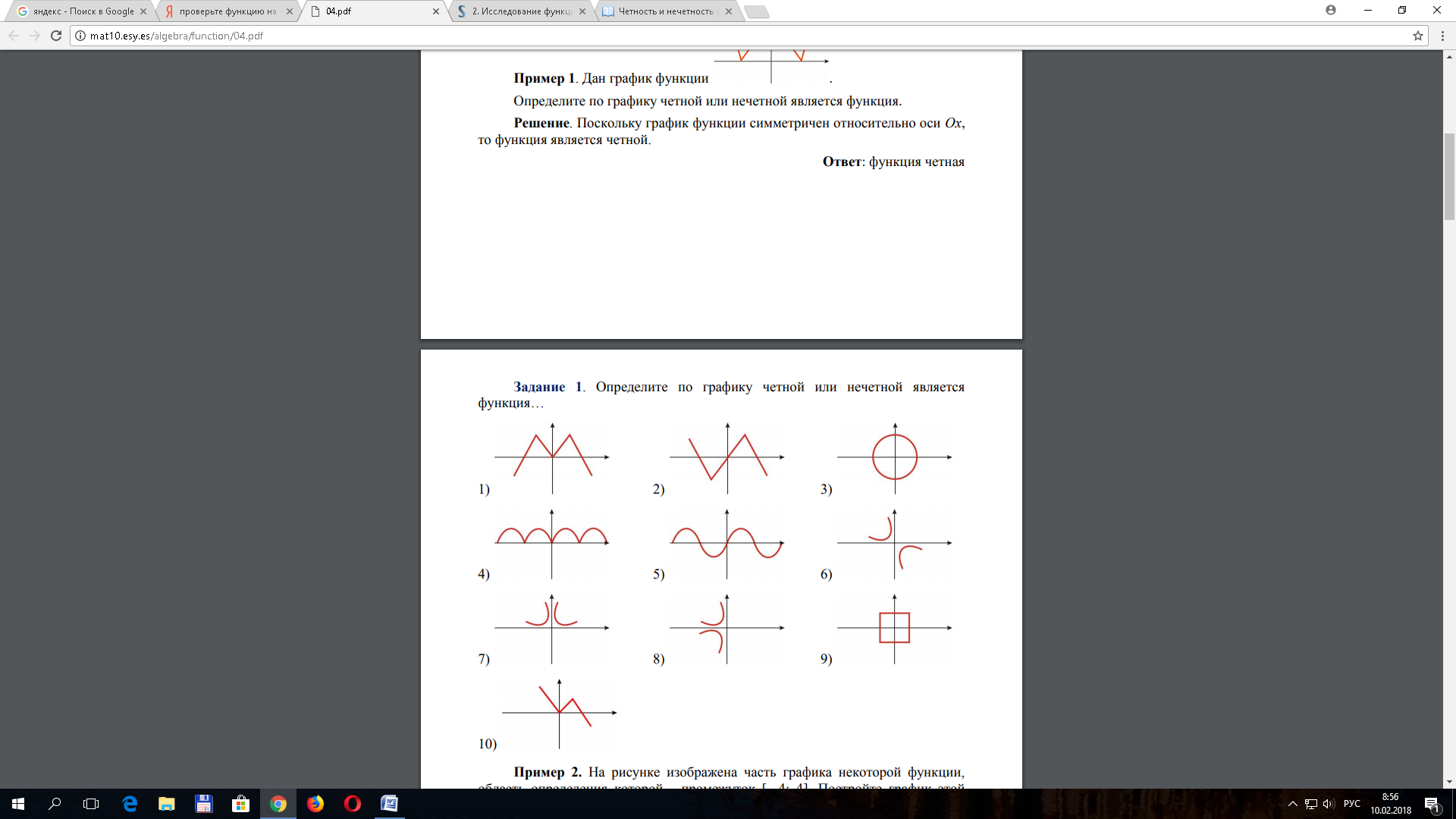
Задание 2. Проверьте функцию на четность (нечетность):

а) f(x)=3х⁴-2х ; б) f(x)=2х⁶-5х²

Задание 3. Исследуйте функцию:

III. Изучение нового материала.

1) Пусть функция у= 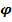(х), заданная на множестве Х и принимает значения У. Функция х= 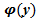, называется обратной функцией к функции у= 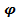(х) (обозначается f^-1).

D( 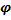): У

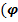Е ): Х

Например: у=f(x)=2x-7

2x=y+7

x= 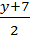, т.е. х=f(у)= .

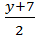2) Рассмотрим какую-нибудь квадратичную функцию, например у=х².

Несложно заметить, что у этой функции не существует обратной: в самом деле, если мы знаем что х²=9 , мы не можем только по этой информации восстановить значение х , возможно два различных варианта х=3и х=-3 . Если бы мы попробовали решить задачу аналитически, то упёрлись бы в ту же проблему: уравнение х²=9 имеет два вещественных корня х=3 и х=-3.

Итак, функция обратной у=х² – не существует, это мы установили. С другой стороны, мы хорошо знаем и ловко пользуемся этой, вроде бы не существующей, функцией. Действительно, для нахождения числа, квадрат которого равен, мы используем квадратный корень, хорошо знакомый нам ещё из школы. Как же мы решили проблему несуществования обратной функции? Или «квадратный корень» вовсе не функция? Здесь мы используем один полезный и простой трюк. Рассмотрим функцию у=х² не на всей оси действительных чисел, а только на положительной полуоси. Здесь по значению функции значение аргумента восстанавливается однозначно, т.е. обратная функция существует! И правда, если мы знаем, что х²=9 и 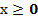, то х=3.

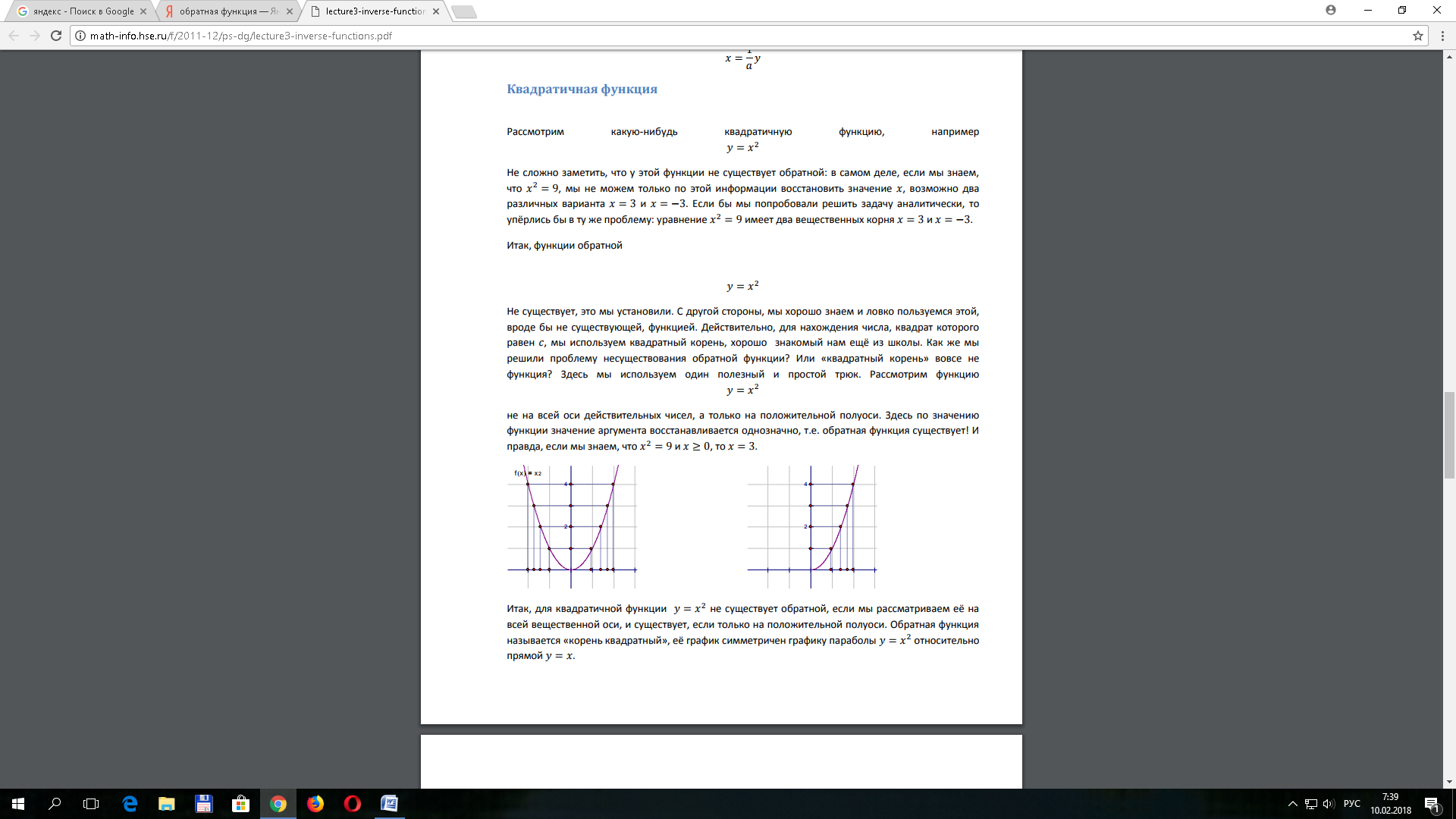
Итак, для квадратичной функции у=х²не существует обратной, если мы рассматриваем её на всей вещественной оси, и существует, если только на положительной полуоси. Обратная функция называется «корень квадратный», её график симметричен графику параболы у=х²относительно прямой у=х.

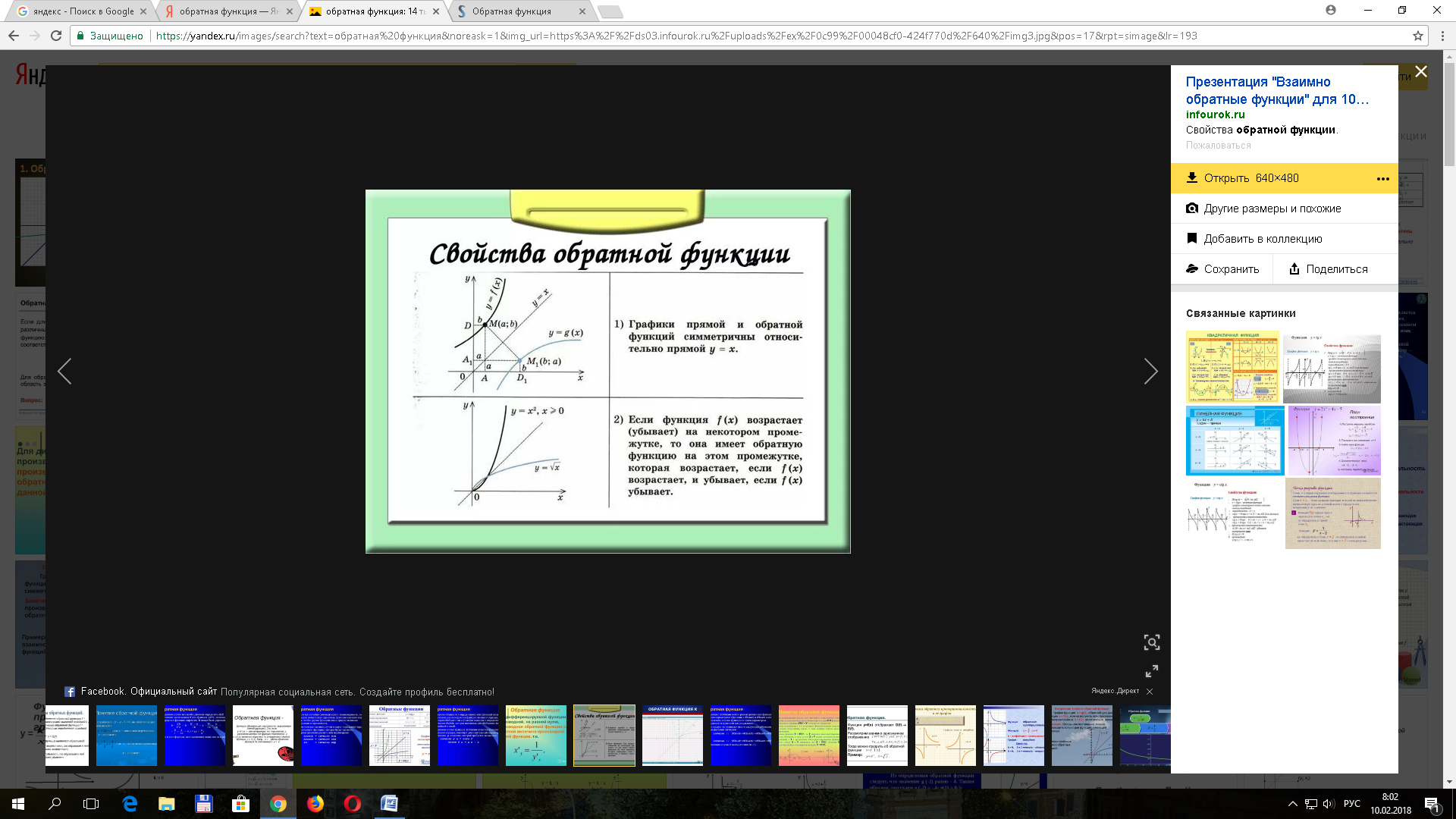Таким образом функции у=х²иу= 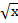- обратные функции.

Свойства обратных функций:

12 Следующая ⇒