Примеры. Пример: y = |x2 - 4|.

Примеры

а) y = –x, Е: R, или y – любое число.

б) y = –x, x [–1; 1]. Е: [–1; 1].

в) y = x² – 1, E: [–1; +∞).

г) y = –x² + 2x, x [0; 3], Е: [–3; 1]

Построим :

Для построения графика функции y = |f(x)| для всех x из области определения, надо ту часть графика функции y = f(x), которая располагается ниже оси абсцисс

(f(x) < 0), отразить симметрично этой оси.

Таким образом, график функции y = |f(x)| расположен только в верхней полуплоскости.

Пример: y = |x2 - 4|.

Строим график функции y = x² – 4

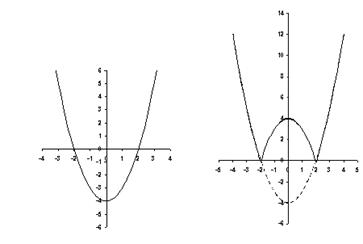
Как правило, учащиеся хорошо понимают правило построения графика такой функции. Его можно легко довести до автоматизма. Во избежание формализма в знаниях и умениях учащихся необходимо чередовать построение графиков вида y = f(|x|) и y = |f(x)|.

С построением графиков зависимостей вида |y| = f(x) учащихся можно познакомить на внеклассных занятиях, ибо такие графики вызывают наибольшие затруднения. Учитывая, что в формуле |y| = f(x) f(x) ≥ 0 и на основании определения модуля

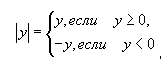
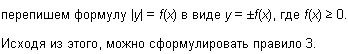
Правило: для построения графиков зависимости (а не функции) достаточно построить график функции y = f(x) для тех x из области определения, при которых f(x) ≥ 0 и отразить полученную часть графика, симметрично оси абсцисс.

Таким образом, график зависимости |y| = f(x) состоит из графиков двух функций: y = f(x) и y = -f(x), где f(x) ≥ 0.

⇐ Предыдущая 12