Свойства дисперсии.. VI. Закрепление нового материала

Свойства дисперсии.

1. Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат.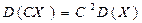

2. Дисперсия суммы двух независимых случайных величин равна сумме дисперсий этих величин.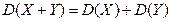

3. Дисперсия разности двух независимых случайных величин равна сумме дисперсий этих величин.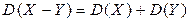

4. Дисперсия постоянной величины равна нулю.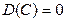

Средним квадратическим отклонением (стандартным отклонением или стандартом) 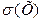дискретной случайной величины Х называется арифметическое значение корня квадратного из ее дисперсии:

= .

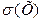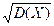Слайд с разобранным решением.

VI. Закрепление нового материала

Работа у доски:

Пример 1: Известно, что М(Х)=5, М(Y)=2. Найти математическое ожидание случайной величины Z=6X-2Y+9-XY.

Решение: М(Z)=6М(Х)-2М(Y)+9-M(X)M(Y)=30-4+9-10=25.

Пример 2: Известно, что D(Х)=5, D(Y)=2. Найти дисперсию случайной величины Z=6X-2Y+9.

Решение: D(Z)=6² D(Х)-2² D(Y)+0=180-8=172.

Пример 3: Известны законы распределений случайных величин Х и Y – оценок, полученных 1 и 2 студентами по теории вероятности.

Х:

x_i
p_i	0, 1	0,2	0,3	0,25	0,15

y_i
p_i	0, 2	0,175	0,15	0,175	0,3

Необходимо выяснить, какой из двух студентов учится лучше. Глядя на ряды распределений их оценок на данный вопрос ответить не просто. У первого студента вероятности получения промежуточных значений (2,3,4) достаточно большие. А у второго студента велики вероятности получения крайних оценок (1и5). Из двух студентов лучше тот, кто чей балл в среднем выше. Таким средним значением случайной величины Х является ее математическое ожидание.

Решение:

По формуле 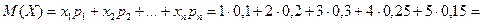3,15.

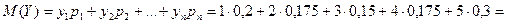2,65.

Т.е. второй студент учится в среднем хуже первого.

Пример4:

1.Дан ряд распределения случайной величины Х.

x_i

p_i 0,4 0,3 0,1 0,2

Найти математическое ожидание , дисперсию и среднее квадратическое отклонение случайной величины случайной величины Х.

Решение:

.

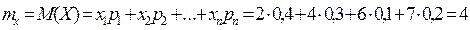Применим формулу 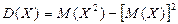для нашего примера:

x_i

x_i²

p_i 0,4 0,3 0,1 0,2

.

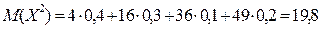
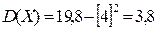Среднее квадратическое отклонение = .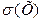

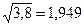Задачи для решения:

1. Дан ряд распределения дискретной случайной величины X:

Найти моду.

2. Контрольная работа состоит из трех вопросов. На каждый вопрос приведено 3 ответа, один из которых правильный. Составить закон распределения числа правильных ответов при простом угадывании. Найти математическое ожидание и дисперсию этой случайной величины.

3. В билете две задачи. Вероятность правильного решения первой задачи равна 0,9, второй – 0,8. Составить закон распределения числа правильно решенных задач в билете и вычислить математическое ожидание и дисперсию этой случайной величины.

4. Построить ряд распределения и функцию распределения случайного числа попаданий мячом в корзину при одном броске, если вероятность попадания мячом в корзину при одном броске p=0,3.

2. Разбор примеров у доски

⇐ Предыдущая 12