
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Свойства математического ожидания.
Тема: «Числовые характеристики дискретной случайной величины»
Случайная величина -величина, которая в результате опыта может принимать то или иное значение, причём до завершения опыта неизвестно какое.
Дискретная случайная величина -величина, которая может принимать отдельные, изолированные значения с определенными вероятностями
Закон распределения -любое правило, устанавливающее соответствие между значениями случайной величины и вероятностями ее наступления
Ряд распределения - совокупность всех возможных значений xi и соответствующих им вероятностей pi.
Многоугольник распределения -графическое изображение ряда распределения , ломаная линия, узлами которой являются точки (xi;рi).
Математическое ожидание – это одно из важнейших понятий в математической статистике и теории вероятностей, характеризующее распределение значений или вероятностей случайной величины. Обычно выражается как средневзвешенное значение всех возможных параметров случайной величины. Широко применяется при проведении технического анализа, исследовании числовых рядов, изучении непрерывных и продолжительных процессов. Имеет важное значение при оценке рисков, прогнозировании ценовых показателей при торговле на финансовых рынках, используется при разработке стратегий и методов игровой тактики в теории азартных игр.
Математическим ожиданием (или средним значением) 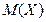 (или
(или 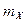 ) дискретной случайной величины X называется сумма произведений всех ее возможных значений на соответствующие вероятности этих значений.
) дискретной случайной величины X называется сумма произведений всех ее возможных значений на соответствующие вероятности этих значений.
Если дискретная случайная величина X принимает конечное число значений 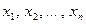 , то ее математическое ожидание
, то ее математическое ожидание 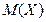 находится по формуле
находится по формуле
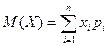
Свойства математического ожидания.
1. Математическое ожидание постоянной величины равно самой постоянной. 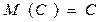
2. Постоянный множитель можно выносить за знак математического ожидания. 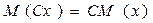
3. Математическое ожидание произведения двух независимых случайных величин равно произведению их математических ожиданий. 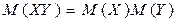
4. Математическое ожидание суммы двух случайных величин равно сумме математических ожиданий слагаемых. 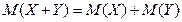
Математическое ожидание не может в достаточной мере охарактеризовать случайную величину, поэтому необходимо использовать такую характеристику как дисперсия.
Дисперсией (рассеиванием) дискретной случайной величины называется математическое ожидание квадрата отклонения случайной величины от ее математического ожидания. 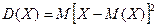
Теорема: Дисперсия равна разности между математическим ожиданием квадрата случайной величины Х и квадратом ее математического ожидания. 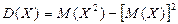
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|