
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Тема урока: «Примеры применения интеграла в физике и геометрии»
Тема урока: «Примеры применения интеграла в физике и геометрии»
| | |
Математика
| Физика
|
Площадь всякой плоской фигуры, рассматриваемая в прямоугольной системе координат, может быть составлена из площадей криволинейных трапеций, прилежащих к оси Ох и оси Оу. Площадь криволинейной трапеции, ограниченной кривой у = f(х), осью Ох и двумя прямыми х=а и х=b, где а 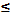 х
х 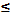 b, f(х)
b, f(х) 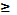 0 вычисляется по формуле
0 вычисляется по формуле 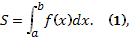 см. рис. Если криволинейная трапеция прилегает к оси Оу, то её площадь вычисляется по формуле
см. рис. Если криволинейная трапеция прилегает к оси Оу, то её площадь вычисляется по формуле 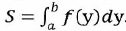 , см. рис. При вычислении площадей фигур могут представиться следующие случаи: а)Фигура расположена над осью Ох и ограничена осью Ох, кривой у=f(х) и двумя прямыми х=а и х=b.(См. рис.) Площадь этой фигуры находится по формуле 1 или 2. б) Фигура расположена под осью Ох и ограничена осью Ох, кривой у=f(х) и двумя прямыми х=а и х=b (см. рис.). Площадь находится по формуле
, см. рис. При вычислении площадей фигур могут представиться следующие случаи: а)Фигура расположена над осью Ох и ограничена осью Ох, кривой у=f(х) и двумя прямыми х=а и х=b.(См. рис.) Площадь этой фигуры находится по формуле 1 или 2. б) Фигура расположена под осью Ох и ограничена осью Ох, кривой у=f(х) и двумя прямыми х=а и х=b (см. рис.). Площадь находится по формуле 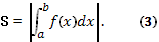 . в) Фигура расположена над и под осью Ох и ограничена осью Ох, кривой у=f(х) и двумя прямыми х=а и х=b(рис.). г) Площадь ограничена двумя пересекающимися кривыми у=f(х) и у =
. в) Фигура расположена над и под осью Ох и ограничена осью Ох, кривой у=f(х) и двумя прямыми х=а и х=b(рис.). г) Площадь ограничена двумя пересекающимися кривыми у=f(х) и у = 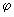 (х) (рис.)
(х) (рис.)
5 ученик: Решим задачу
х-2у+4=0 и х+у-5+0 и у=0
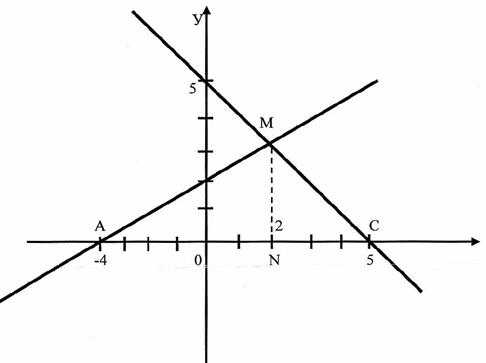
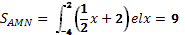
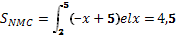
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|
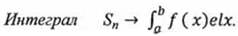 при
при 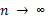 .
.