Математическое ожидание случайной величины

Математическое ожидание случайной величины

Как мы знаем, распределение вероятностей случайной величины — это таблица, в которой указаны значения случайной величины и их вероятности. Для практики не всегда нужно изучать всю таблицу распределения. Достаточно знать некоторые ее числовые характеристики. Рассмотрим случайную величину X. Ее математическое ожидание обычно обозначают Е(Х).Пусть распределение вероятностей случайной величины X задано таблицей:

Значение величины X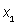
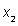
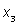
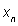
Вероятность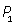

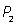
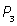
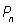
Математическим ожиданием случайной величины X называют число

Е(Х)= х₁ · Р₁ + х₂ · Р₂ + … + х_n · Р_n.

Математическое ожидание Е(Х) называют также ожидаемым значением случайной величины X, средним значением случайной величины X. Если значения случайной величины измеряются в каких-либо единицах (например, рост — в сантиметрах, температура — в градусах), то ее математическое ожидание измеряется в этих же единицах (средний рост — в сантиметрах, средняя температура — в градусах)

Пример 3. Для проведения лотереи изготовили 100 билетов. Из них 1 билет с выигрышем в 500 р., 10 билетов с выигрышами по 100 р. и остальные 89 билетов без выигрышей. Наудачу выбирают один билет. Найдем математическое ожидание выигрыша M(X).

Количество билетов
Выигрыш	500 руб.	100 руб.	0 руб
Вероятность	1/100	1/10	89/100

Эта случайная величина может принимать три значения: 500 р., 100 р. и 0 р. (нет выигрыша). Их вероятности равны 0,01, 0,10 и 0,89. Математическое ожидание выигрыша равно 500 · 0,01 + 100 · 0,10 + 0 · 0,89 = 15 (р.). Получается, что средний выигрыш на один билет равен 15 р.

Для того чтобы лотерея приносила доход своим устроителям, цена билета должна быть больше, чем средний выигрыш. Предположим, что билет стоит 20 р. Продав все билеты, устроители лотереи получат 2000 рублей.

На выплату выигрышей будет потрачено 1500 рублей.

Таким образом, доход от лотереи составит 500 рублей.

Разумеется, может случиться так, что на один купленный нами билет мы получим большой выигрыш. Но если бы некто решил купить все билеты, то он достоверно потерял бы 500 рублей — по 5 на каждый из 100 билетов.

Так устроены все лотереи: математическое ожидание выигрыша на один билет меньше цены этого билета.

Это условие является непременным, и оно обеспечивает рентабельность лотереи и доход ее устроителям. Человек, который решил сыграть в лотерею, должен понимать это и сознательно рисковать своими деньгами.

⇐ Предыдущая 1 234 Следующая ⇒