Размах. Дисперсия. Среднеквадратичное отклонение

Размах. Дисперсия. Среднеквадратичное отклонение

Средние характеристики числового ряда позволяют оценить его поведение «в среднем». Но это далеко не всегда полностью характеризует выборку.

Размах — это разность наибольшего и наименьшего значений ряда данных: …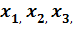

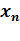
R =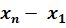

Пример 4. Температура на Меркурии колеблется от - 150 до + 350 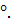Удобен ли климат Меркурия для жизни людей, если на планете Меркурий средняя температура +15 ?

Например, на планете Меркурий средняя температура +15°. Исходя из этого статистического показателя, можно подумать, что на Меркурии умеренный климат, удобный для жизни людей.

Однако на самом деле это не так. Температура на Меркурии колеблется от — 150° до +350°.

Значит, чтобы получить представление о поведении числового ряда, помимо средних характеристик надо знать характеристики разброса, показывающие, насколько значения ряда различаются между собой, как сильно они «разбросаны» вокруг средних. Простейшей такой характеристикой является размах.

Для температуры на Меркурии, например, размах равен

350° — (-150°) = 500°. Конечно, такого перепада температур человек выдержать не может.

Размах очень просто вычисляется, но не всегда несет достоверную информацию, так как на его величину может сильно повлиять какое-то одно (возможно, ошибочное) значение статистического ряда.

Вот почему в реальных статистических исследованиях чаще используют другую характеристику разброса, которая сложнее вычисляется, но зато меньше подвержена таким колебаниям.

Прежде чем определять эту величину, рассмотрим на примере, какой самый естественный способ вычисления «среднего отклонения от среднего».

Пример 2. Дан числовой ряд, который представляет собой стоимость одного литра бензина на 10 автозаправочных станциях (в рублях):

32,2; 32,8; 33; 32,9; 33; 32,5; 32,8; 33; 33,2; 32,8.

Найдем среднее арифметическое этих цен:

(32,2 + 32,8 + 33 + 32,9 + 33 + 32,5 + 32,8 + 33+ 33,2 + 32,8 ) / 10 = 32,82.

Самым естественным, на первый взгляд, кажется посчитать отклонение от среднего для каждого члена ряда и затем найти их среднее арифметическое:

((32,2 - 32,82) + (32,8 - 32,82) +(33- 32,82) + … + (32,8 - 32,82)) / 10 = 0.

Мы получили нуль совсем не случайно: при вычислении «среднего разброса» по такой формуле часть отклонений входит в сумму со знаком «плюс», часть — со знаком «минус», а в сумме всегда получается нуль.

Какой же выход? Можно суммировать, например, модули отклонений — тогда уж нуля точно не будет. Иногда так и поступают, но с модулем не всегда удобно работать. Поэтому математики решили, что лучше складывать не модули отклонений, а их квадраты — они ведь тоже неотрицательные.

Так появилось понятие дисперсии числового ряда.

Дисперсией числового ряда называется среднее арифметическое квадратов отклонений от среднего арифметического.

D =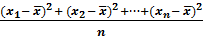

Найдем дисперсию числового ряда из нашего примера с ценами на бензин. Среднее арифметическое мы уже вычислили — оно равно32,82.

Найдем теперь дисперсию, т. е. среднее арифметическое квадратов отклонений от среднего:

((32,2 - 32,82)² + (32,8 - 32,82)² + (33 - 32,82)² + … + (32,8 - 32,82)² ) / 10 = 0,0736.

У дисперсии есть один существенный недостаток: если исходные значения ряда измеряются в каких-то единицах (например, в рублях), то у дисперсии эти единицы возводятся в квадрат («квадратные» рубли).

В нашем примере среднее значение цены получилось 32 рубля 82 копейки, а вот дисперсия цен — около 7 … «квадратных копеек».

Избавиться от таких странных единиц измерения можно, если использовать другую характеристику разброса — стандартное отклонение.

Стандартным (или средним квадратичным) отклонением числового ряда называется квадратный корень из дисперсии: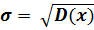

Обозначают его греческой буквой 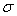(«сигма»). В рассмотренном примере стандартное отклонение будет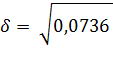 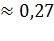, т.е. приблизительно 27 коп.

Как и при изучении средних характеристик, попробуем найти характеристики разброса по таблице частот.

⇐ Предыдущая 123 4 Следующая ⇒