
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
при любом значении . Вертикальные плоскости и пересекают однополостный гиперболоид, соответственно, по гиперболам
при любом значении . Вертикальные плоскости и пересекают однополостный гиперболоид, соответственно, по гиперболам
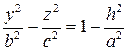 и
и 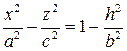 .
.
В зависимости от знака правой части уравнений направление ветвей гипербол изменяется, в случае равенства правой части нулю получим уравнения пересекающихся прямых. При условии 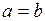 однополостный гиперболоид образуется вращением гиперболы относительно оси аппликат. Однополостный гиперболоид является линейчатой поверхностью: через каждую его точку проходят две пересекающиеся прямые, лежащие на гиперболоиде.
однополостный гиперболоид образуется вращением гиперболы относительно оси аппликат. Однополостный гиперболоид является линейчатой поверхностью: через каждую его точку проходят две пересекающиеся прямые, лежащие на гиперболоиде.
Двуполостной гиперболоид имеет каноническое уравнение
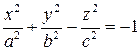 .
.
Заметим, что горизонтальные плоскости 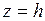 пересекают двуполостный гиперболоид лишь при условии
пересекают двуполостный гиперболоид лишь при условии 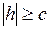 . В отличие от однополостного гиперболоида, прямолинейных образующих двуполостный гиперболоид не имеет.
. В отличие от однополостного гиперболоида, прямолинейных образующих двуполостный гиперболоид не имеет.
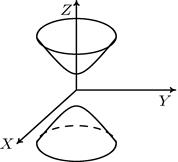
Рис. 3. Двуполостной гиперболоид
Конус имеет каноническое уравнение
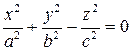
и при 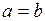 является конусом вращения, или круговым конусом.
является конусом вращения, или круговым конусом.
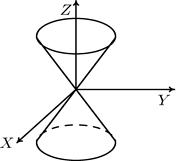
Рис.4. Конус
Координатные плоскости 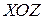 и
и 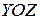 пересекают конус, соответственно, по прямым
пересекают конус, соответственно, по прямым
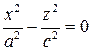 ,
, 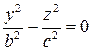 .
.
Интересно, что при сечении конуса различными плоскостями получаются все типы невырожденных линий второго порядка: эллипсы, гиперболы и параболы.
Эллиптический параболоид имеет каноническое уравнение
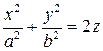 .
.
Горизонтальные сечения эллиптического параболоида плоскостями 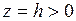 – эллипсы, вертикальные сечения – параболы. При условии
– эллипсы, вертикальные сечения – параболы. При условии 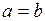 эллиптический параболоид является поверхностью вращения.
эллиптический параболоид является поверхностью вращения.
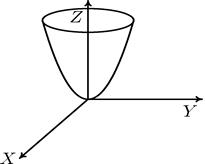
Рис.5. Эллиптический параболоид
Гиперболический параболоид имеет каноническое уравнение
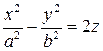 .
.
Горизонтальные сечения этой поверхности – гиперболы с различным направлением ветвей и пересекающиеся прямые в плоскости XOY. Вертикальные сечения, параллельные координатным плоскостям, – параболы. Как и однополостный гиперболоид, эта поверхность является линейчатой, т.е. имеет прямолинейные образующие.
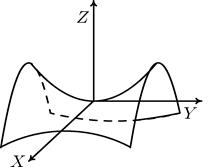
Рис. 6. Гиперболический параболоид
Канонические уравнения цилиндрических поверхностей содержат только две переменные, 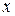 и
и 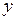 . Следовательно, сечения цилиндрических поверхностей плоскостями
. Следовательно, сечения цилиндрических поверхностей плоскостями 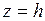 одинаковы и не зависят от значения
одинаковы и не зависят от значения 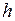 . Цилиндрические поверхности второго порядка задаются следующими каноническими уравнениями:
. Цилиндрические поверхности второго порядка задаются следующими каноническими уравнениями:
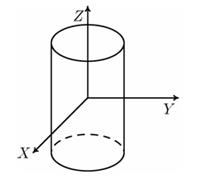
Рис.7. Эллиптический цилиндр
Каноническое уравнение эллиптического цилиндра
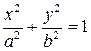 .
.

Рис.8. Гиперболический цилиндр
Каноническое уравнение гиперболического цилиндра
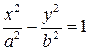 .
.
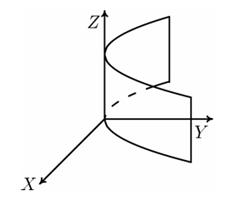
Рис. 9. Параболический цилиндр
Каноническое уравнение параболического цилиндра
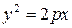 .
.
Вопросы для самопроверки
1. Что называется поверхностью второго порядка?
2. Какие основные типы невырожденных поверхностей второго порядка?
3. Каковы канонические уравнения эллипсоида, одно и двуполостного гиперболоидов?
4. Каковы канонические уравнения конуса, эллиптического и гиперболического параболоидов?
5. Каковы канонические уравнения цилиндрических поверхностей?
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|