
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Тоді з рівності
Контрольна робота № 9
І. Знайти найбільший спільний дільник многочленів f(x) і g(x) та підібрати такі многочлени m(x) і n(x), що f(x)m(x) + g(x)n(x) = d(x).
2) f(x) = x6 – 7x4 + 8x3 – 7x + 7; g(x) = 3x5 – 7x3 + 3x2 – 7;
Розв‘язання.
До многочленів f(x) і g(x) застосовуємо алгоритм Евкліда:
| _ x6 – 7x4 + 8x3 – 7x + 7 | 3x5 – 7x3 + 3x2 – 7 |
|
|
| |||||||||||||
| x6 – |
|
|
| ||||||||||||||
|
| - |
|
|
|
| ||||||||||||
|
|
|
|
|
|
| ||||||||||||
| _ 3x5 – 7x3 + 3x2 – 7 | - |
|
|
| |||||||||||||
| 3x5 –9/2 x4+3x2 - 9/2x |
|
|
|
| |||||||||||||
|
| _ 9/2 x4 - 7x3 + 9/2x – 7 |
|
|
|
| ||||||||||||
|
| 9/2x4 – 27/49x3 + 9/2x - 27/4 |
|
|
|
| ||||||||||||
|
| -1/4x3 - 1/4 |
|
|
|
| ||||||||||||
|
|
|
|
|
|
| ||||||||||||
| 14/3x4 + 7х3– 14/3x + 7 | -1/4x3 - 1/4 |
|
|
|
| ||||||||||||
| 14/3x4 – 14/3x |
|
|
|
|
| ||||||||||||
| _ 7х3 - 7 |
|
|
|
| |||||||||||||
| 7х3 + 7 |
|
|
|
| |||||||||||||
| – 14. |
|
|
|
| |||||||||||||
Отже, в результаті ділення одержуємо:
f(x) = g(x)q1(x) + r1(x);
q1(x) = 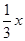 , r1(x) = -
, r1(x) = - 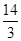 x4 + 7x3 –
x4 + 7x3 – 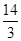 x +7;
x +7;
g(x) = r1(x)q2(x) + r2(x);
q2(x) = 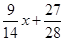 ; r2(x) =
; r2(x) = 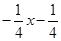 ;
;
r1(x) = r2(x)q3(x) + r3(x);
q3(x) = 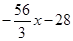 ; r3(x) = –14.
; r3(x) = –14.
Так як r3(x) = –14 є стале число, а на стале число без остачі ділиться будь-який многочлен, то наступна остача r4(x) буде дорівнювати нулю. Отже, алгоритм Евкліда записався тут у три рядки, а найбільший спільний дільник дорівнює – 14, або
d(x) = 1 = – 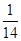 r3(x).
r3(x).
Щоб виразити d(x) через многочлени m(x) і n(x) виразимо спочатку через них r3(x).
r3(x) = r1(x) – r2(x) q3(x),
r3(x) = r1(x) – [g(x) – r1(x)q2(x)]q3(x),
або r3(x) = r1(x)[1 + q2(x)q3(x)] – g(x)q3(x).
В останню рівність замість r1(x) підставимо його вираз з першого рядка алгоритму Евкліда, одержимо:
r3(x) = [f(x) – g(x)q1(x)]×[1 + q2(x)q3(x)] – g(x)q3(x) =
= –f(x)[1 + q2(x)q3(x)] + g(x)[–q1(x) – q1(x)q2(x)q3(x) – q3(x)].
Враховуючи, що d(x) = – 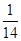 r3(x), маємо:
r3(x), маємо:
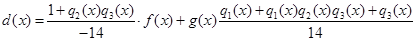 .
.
Отже, 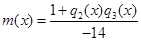 ;
;
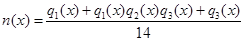 ,
,
де q1(x) = 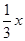 ; q2(x) =
; q2(x) = 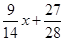 ; q3(x) =
; q3(x) = 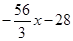 .
.
Одержуємо: 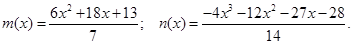
Відповідь: 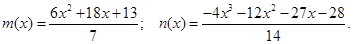
ІІ. Користуючись схемою Горнера:
а) розкласти многочлен f(x) за степенями (х – а) і одержаний розклад розташувати за спадними степенями х;
б) знайти канонічний розклад (відокремити кратні множники);
в) знайти значення многочлена f(x) та його похідних при х = а, якщо
f(x) = x5 + 3x4 – 9x3 – 7x2 + 39x – 21, a = 1.
Розв‘язання.
а) За схемою Горнера маємо:
| -9 | -7 | -21 | ||||
| -5 | -12 | |||||
| -12 | ||||||
| -6 | ||||||
Звідси
f(x) = (x – 1)5 + 8(x – 1)4 + 13(x – 1)3 – 6(x – 1)2 + 15(x – 1) + 6 = F(x – 1).
Розташуємо многочлен F(x – 1) за степенями х. запишемо х у вигляді
x = (x – 1) + 1 і за схемою Горнера розділимо F(x – 1) на двочлен (x – 1) + 1, одержуємо:
| -6 | ||||||
| -12 | -21 | |||||
| -12 | ||||||
| -5 | -7 | |||||
| -9 | ||||||
Отже, F(x –1) = x5 + 3x4 – 9x3 – 7x2 + 39x – 21.
б) Знайдемо d1 = (f, f¢ ), де f¢ = 5x4 + 12x3 – 27x2 – 14x + 39.
в) Для многочлена f(x) запишемо формулу Тейлора:
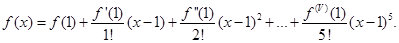
Порівняємо формулу з розкладом за степенями (х - 1). Одержуємо:
f(1) = 6; f ¢(1) = 15; f ¢¢(1) = 2!×(-6);
f ¢¢¢(1) = 3!×13; f (IV) (1) = 4!×8; f (V) (1) = 5!×1.
ІІІ. Знайти раціональні корені многочлена
f(x) = 6x4 + 19x3 - 7x2 - 26x + 12.
Розв‘язання.
Старший коефіцієнт a0 = 6 ¹ 1. Тому многочлен, якщо має раціональні корені, то вони можуть бути як цілими, так і дробовими.
Шукаємо їх серед чисел:
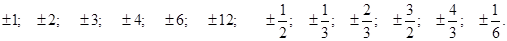
Знайдемо границі дійсних коренів многочлена 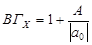
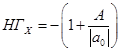
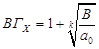
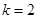 , В = 26, а0 = 6,
, В = 26, а0 = 6, 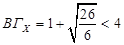
Знаходження нижньої границі: f(x-) = 6x4 - 19x3 - 7x2 + 26x + 12
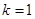 , В = 19, а0 = 6,
, В = 19, а0 = 6, 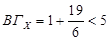
Нижня границя НГХ = -5. Корні многочлена знаходяться в інтервалі (-5;4).
Використаємо, те що якщо 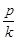 - корінь
- корінь 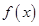 , то
, то 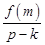 ціле. Знайдемо
ціле. Знайдемо 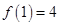 ,
, 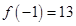 значить
значить 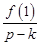 - ціле,
- ціле, 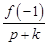 - ціле, якщо
- ціле, якщо 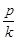 - корінь
- корінь 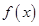 .
.
Перевіримо усілякі дробі 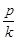 , ураховуючи границі коренів
, ураховуючи границі коренів
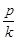
| 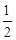
| - 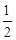
| 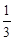
| 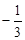
| 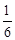
| - 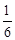
| 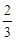
| - 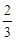
| 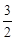
| - 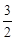
| 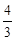
| - 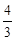
| -2 | -3 | -4 | |||
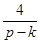
| ц | д | ц | ц | д | д | ц | д | ц | д | ц | д | ц | д | ц | ц | д | д |
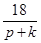
| ц | д | ц | д | д | д | ц | д | ц |
З’явилися «кандидати в корені», це числа 2, -3, 1/3, 1/2.Перевіряючи їх за схемою Горнера переконуємося, що 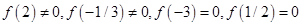 . Для многочлена четвертого ступеня знайшли два кореня:
. Для многочлена четвертого ступеня знайшли два кореня: 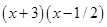 або
або 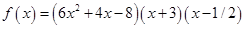 .
.
Корені многочлена 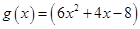 знаходимо безпосередньо
знаходимо безпосередньо
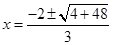 - не раціональне.
- не раціональне.
ІV. Виразити через елементарні симетричні многочлени многочлен.
f(x1, x2, x3) = x15x2x3 + x25x1x3 + x35x1x2 + 2x1x2x3.
Розв‘язання.
Складемо розрахункову таблицю:
| Система показників вищого члена | Вищий член | Відповідна комбінація елементарних симетричних многочленів |
| 5 1 1 | x15x2x3 | s14s3 |
| 4 2 1 | bx14x22x31 | bs12s2s3 |
| 3 2 2 | cx13x22 x32 | cs1s3 |
Тоді f(x1, x2, x3) = s14s3+ bs12s2s3+ cs1s3, (*)
де s1 = x1 + x2 + x3, s2 = x1x2 + x1x3 + x2 x3, s3 = x1x2 x3.
Поклавши x1 = 1; x2 = 1; x3 = -2, одержуємо: s1 = 0, s2 = -3, s3= -2, f = –40.
Підставляючи знайдені значення у вираз (*), одержуємо:
–40 = b × (–2); b = 20,
тобто f(x1, x2, x3) = s14s3+ 20s12s2s3+ cs1s3(**)
Надаємо значень x1 = x2 = 1, x3 = –1, одержуємо:
s1 = 1, s2 = –1, s3 = –1, f = –5.
Підставляємо знайдені значення у вираз (**), одержуємо: c = 24. Отже,
f(x1, x2, x3) = s14s3+ 20s12s2s3+ 24s1s3
V. У множині дійсних чисел розв’язати систему рівнянь:
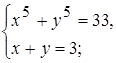
Розв‘язання.
VI. Позбавитися від алгебраїчної ірраціональності в знаменнику дробу
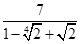 .
.
Розв‘язання.
Заданий дріб є значенням раціонального дробу 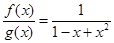 при
при 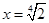 , яке є коренем незвідного у полі Q многочлена h(x) = x4 – 2. Многочлени g(x) і f(x) взаємно прості. Знайдемо лінійне зображення їхнього найбільшого спільного дільника.
, яке є коренем незвідного у полі Q многочлена h(x) = x4 – 2. Многочлени g(x) і f(x) взаємно прості. Знайдемо лінійне зображення їхнього найбільшого спільного дільника.
Ділення многочленів виконаємо “кутом”:
| _ x4 – 2 | x2 – x + 1 | |||||
| x4 – x3 + x2 | x2 + х | |||||
| _ x3 – x2 – 2 | ||||||
| x3 – x2 + х | ||||||
| – x – 2 | ||||||
x4 – 2 = (x2 – x + 1)(x2 + х) – x – 2,
h(x) = g(x)(x2 + х) – (x + 2).
x + 2 = –h(x) + g(x)(x2 + х);
| _ x2 – x + 1 | – x – 2 | |||||
| x2 + 2x | 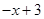
| |||||
| _ – 3x + 1 | ||||||
| – 3x – 6 | ||||||
| 7 | ||||||
x2 – x + 1 = (– x – 2)( 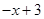 ) + 7,
) + 7,
g(x) = – (x + 2)( 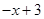 ) + 7.
) + 7.
Звідси
7 = g(x) + (x + 2)( 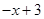 ) = g(x) + (– h(x) + g(x)(x2 + х))(
) = g(x) + (– h(x) + g(x)(x2 + х))( 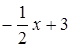 ) =
) =
= g(x)(1 + (x2 + х)( 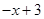 )) + h(x)(
)) + h(x)( 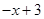 ) =
) =
= g(x)( 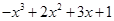 ) + h(x)(
) + h(x)( 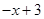 ).
).
Оскільки 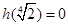 , то
, то

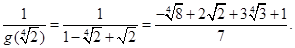
VІІ. Довести, що число a є алгебраїчним і знайти його мінімальний многочлен, якщо 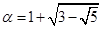 .
.
Розв‘язання.
Число a називають алгебраїчним відносно поля Р, якщо воно є коренем деякого многочлена над полем Р. Отже, нам треба знайти незвідний над полем Р многочлен, коренем якого є число 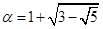 . Для цього розглянемо рівняння
. Для цього розглянемо рівняння 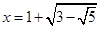 . Число a є коренем цього рівняння. Обидві частини цього рівняння підносимо до другого степеня
. Число a є коренем цього рівняння. Обидві частини цього рівняння підносимо до другого степеня 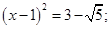 .
.
Позбавляємося від ірраціональних коефіцієнтів:
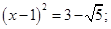
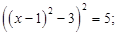 ,
,
звідси одержуємо рівняння з раціональними коефіцієнтами x4 – 4x3 + 8х - 1 = 0.
В результаті зроблених перетворень не відбулося втрати коренів. Отже, число 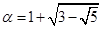 є коренем одержаного рівняння або многочлена
є коренем одержаного рівняння або многочлена
f(x) = x4 – 4x3 + 8х - 1 . Цей многочлен над полем раціональних чисел незвідний. Так як степінь многочлена f(x) дорівнює 4, то число 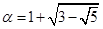 є алгебраїчним числом 4-ого степеня, а його мінімальним многочленом є многочлен
є алгебраїчним числом 4-ого степеня, а його мінімальним многочленом є многочлен
f(x) = x4 – 4x3 + 8х - 1 .
VІІІ. Розкласти на незвідні у полі Q множники многочлен
f(x) = x4 – x3 – 6x2 + 8x – 2.
Розв‘язання.
Нехай многочлен f(x) є звідним у полі Q, тобто його можна розкласти в добуток не менше як двох многочленів ненульового степеня з кільця Q[x]. Щоб розкласти многочлен f(x) на множники, застосуємо метод невизначених коефіцієнтів. При цьому досить розглянути два випадки можливого розкладу:
1) обидва множники мають степінь 2;
2) один множник має степінь 1, а другий 3.
Нехай f(x) = (ax2 + bx + c)(dx2 + mx + n). (1)
Тоді з рівності
x4 – x3 – 6x2 + 8x – 2= adx4 + (am + bd)x3 + (an + bm + cd)x2 + (bn + cn)x + cn
маємо
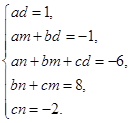 (2)
(2)
Розв‘яжемо цю систему рівнянь в цілих числах. Знаходимо a = d = 1 або
a = d = –1, з останнього рівняння – c = -1, n = 2, c = -2, n = 1, c = 2, n = –1, c = 1, n = –2. Розглянемо кожен з восьми можливих варіантів.
1) Якщо a = d = 1, c = -1, n = 2, то маємо систему:
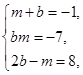 .
.
Ця система несумісна.
2) У кожному з решти варіантів несумісними є також системи рівнянь:
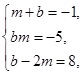
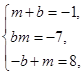
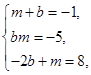
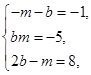
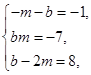
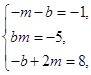
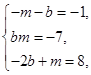
Це означає, що система рівнянь (2) несумісна і многочлен f(x) не розкладається в добуток двох многочленів другого степеня з цілими коефіцієнтами.
Припустимо, що розклад (1) виконується при дробових числах a, b, c, d, m, n. Зведемо до найменшого спільного знаменника коефіцієнти многочленів g1(x) = ax2 + bx + c, g1(x) = dx2 + mx + n та винесемо за дужки ці знаменники і найбільші спільні дільники чисельників обох многочленів. Одержуємо розклад
 ,
,
де (r, s) = (a1, b1, c1) = (d1, m1, n1) = 1.
Оскільки коефіцієнти многочлена f(x) є цілими числами, то всі коефіцієнти многочлена 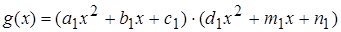 мають ділитися на число s, а тому й на кожен його простий дільник р.
мають ділитися на число s, а тому й на кожен його простий дільник р.
Разом з тим, серед кожної трійки чисел a1, b1, c1 та d1, m1, n1 знайдуться числа, які не діляться на р. тому серед коефіцієнтів a1d1, a1m1 + b1d1,
a1n1 + b1m1 + c1d1, b1n1 + c1m1 і c1n1 многочлена g(x) знайдеться такий, що не ділиться на р. тому s = 1 і ми дістанемо розклад (1) з цілими коефіцієнтами, що неможливо.
Нехай f(x) =(ax + b)(cx3 + dx2 + mx + n). Тоді з рівності
x4 – x3 – 6x2 + 8x – 2 = acx4 + (ad + bc)x3 + (am + bd)x2 + (an + bm)x + bn
маємо:
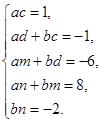
Одним з розв‘язків цієї системи є a = c = 1, n = 2, b = -1, d = 0, m = - 6. Отже, f(x) = (x - 1)(x3 - x2 - 6x + 2). тобто многочлен f(x) звідний у полі Q.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|
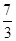 x4 + x3 –
x4 + x3 –