
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Обов’язкове домашнє завдання з предмету „Спецрозділи математики”
Обов’язкове домашнє завдання з предмету „Спецрозділи математики”
Спеціальність СУ Семестр 3
Розділ 1 Елементи дискретної математики
Тема: „Системи числення” (самостійне вивчення)
Завдання 1
а) Перевести числа у двійкову систему.
б) Виконати операції додавання, віднімання, множення, ділення над двійковими числами.
в) Результати перевести до десяткової системи. Зробити перевірку виконання операцій.
г) Результат множення перевести до вісімкової та шістнадцятирічної систем.
| Варіант | Число А | Число В |
| 40.5 | 3.375 | |
| 57.75 | 5.25 | |
| 55.5 | 4.625 | |
| 97.5 | 7.5 | |
| 29.75 | 2.125 | |
| 89.25 | 5.25 | |
| 71.25 | 4.75 | |
| 2.375 | ||
| 5.5 | ||
| 4.375 | ||
| 31.5 | 2.25 | |
| 85.5 | 4.5 | |
| 1.5 | ||
| 5.375 | ||
| 62.5 | 2.5 | |
| 97.75 | 4.25 | |
| 7.75 | ||
| 94.25 | 7.25 | |
| 6.375 | ||
| 94.5 | 4.5 | |
| 81.25 | 6.25 | |
| 7.125 | ||
| 28.5 | 4.75 | |
| 25.5 | 1.5 | |
| 40.5 | 2.25 | |
| 38.5 | 2.75 | |
| 59.5 | 3.5 | |
| 18.5 | 4.625 | |
| 52.5 | 3.5 | |
| 1.625 |
Тема: „Множини”
Завдання 2

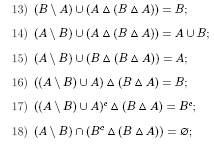

Тема: „Логіка”
Завдання 3-6

Розділ 2 Операційне числення та його додатки
Тема: „Операційне числення”
Завдання 6
6.1 Розвязати диференційне рівняння операційним методом.
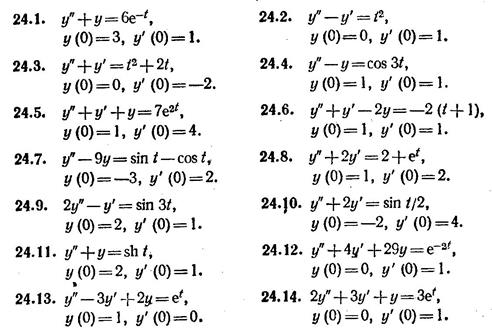
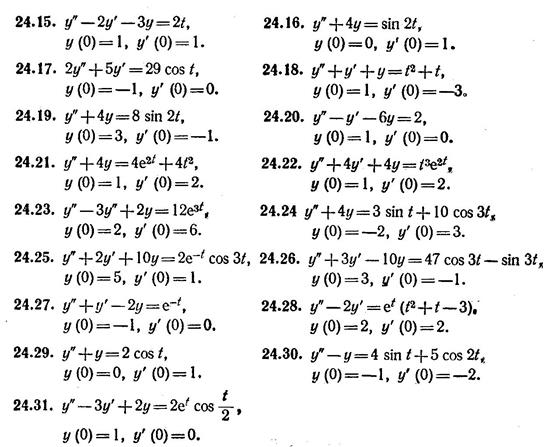
6.2 Розвязати різнистне рівняння при умовах 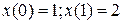
1. 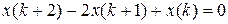
2. 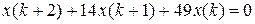
3. 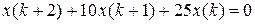
4. 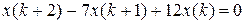
5. 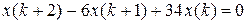
6. 
7. 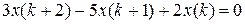
8. 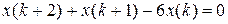
9. 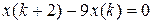
10. 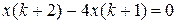
11. 
12. 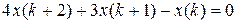
13. 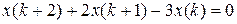
14. 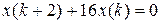
15. 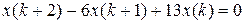
16. 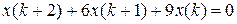
17. 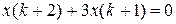
18. 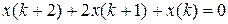
19. 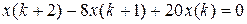
20. 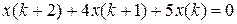
Розділ 3 Елементи теорії графів
Тема: „Графи”
Завдання 7
7.1
Дан неорієнтований граф G(V,E) і орієнтований граф G1(V,E).
Виписати:
а) множину вершин і множину ребер для графа G;
б) списки суміжності для графа G;
в) матрицу весов для графа G1.
7.2
Для неорієнтованого графа G(V,E) виконати „пошук у глиб” та «пошук в шир». Вихідна вершина 1.
7.3
Виконати алгоритм Прима-Краскала („жадний”) та знайти остов мінімальної ваги неорієнтованого графа G.
7.3
Виконуючи алгоритм Дейкстри знайти найкоротший шлях від 1-ої до 10-ї вершини орієнтованого графа G1. Результат представити у вигляді таблиці, за якою можна знайти мінімальний шлях від 1-ї до будь-якої вершини.
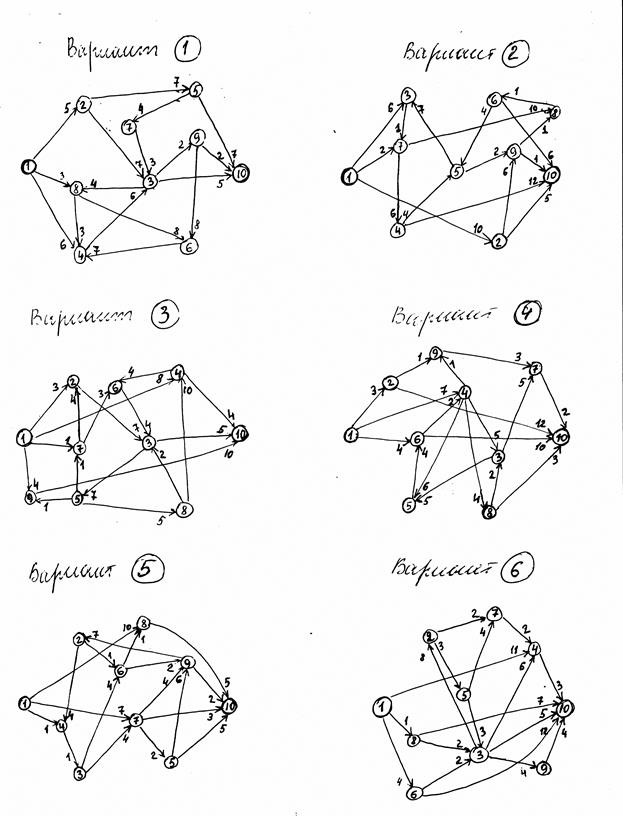
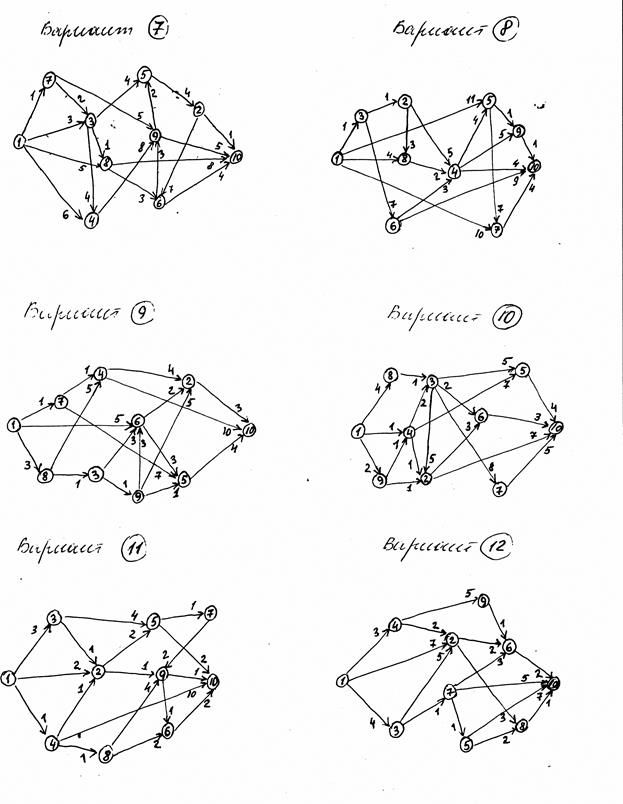
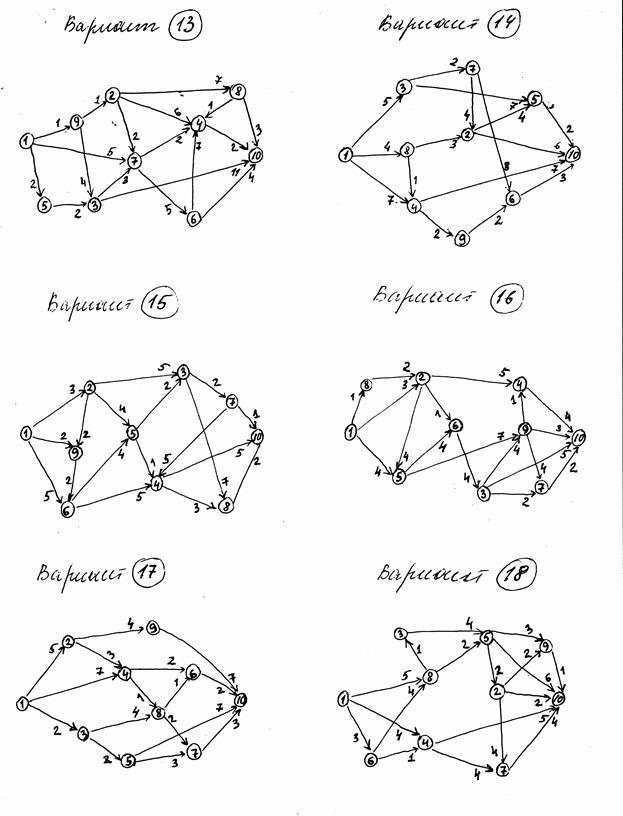
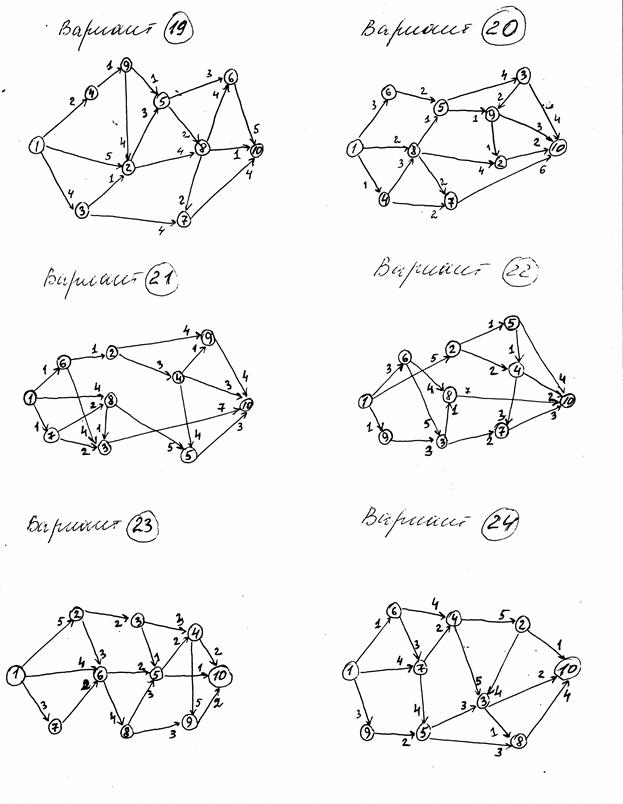
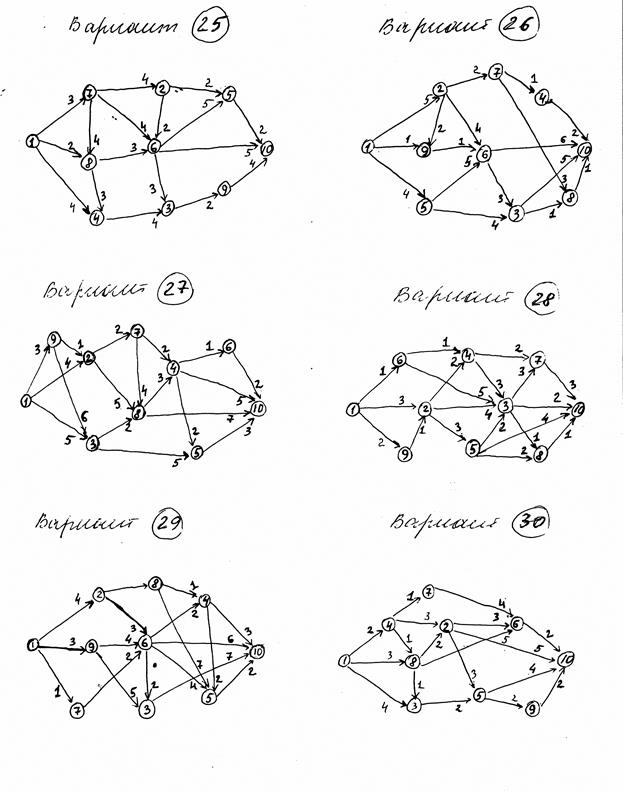
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|