Поверхности второго порядка

Поверхности второго порядка

Поверхности являются пространственными аналогами кривых второго порядка на плоскости.

1. Эллипсоид

Определение. Эллипсоидом называется поверхность, которая в некоторой декартовой системе координат определяется уравнением:

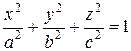- каноническое уравнение эллипсоида. (1)ыв

Постараемся уяснить форму эллипсоида с помощью «метода параллельных сечений».

Рассмотрим сечения данного эллипсоида плоскостями, параллельными Оху, т.е. z=h. Линия, которая получается в сечении, определяется двумя уравнениями:

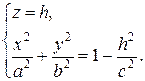(2)

Если: 1) 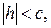то плоскость z=h пересекает эллипсоид (1) по эллипсу с полуосями:

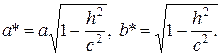
1) Величина 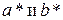имеют наибольшие значения при h=0, иначе говоря, самый крупный эллипсоид получается при сечении координатной плоскостью z=0.

2) При возрастании 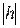величины 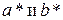уменьшаются.

3) При 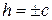величины 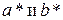обращаются в 0, т.е. сечение эллипса вырождается в точку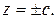

4) При 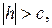уравнения (2) определяют мнимый эллипс, т.е. плоскость z=h с данным эллипсоидом не встречается совсем.

Совершенно аналогично рассматриваются сечения эллипсоида плоскостями, параллельными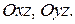

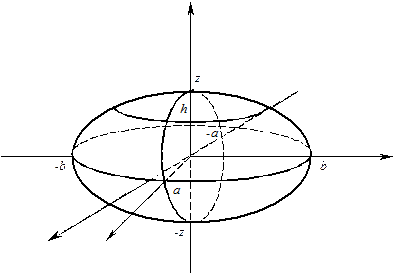
Таким образом, вывод: эллипсоид есть замкнутая овальная поверхность, обладающая тремя взаимно перпендикулярными плоскостями симметрии. Величины 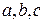называются полуосями эллипсоида. Если все они различны, то эллипсоид называется трехостным.

При 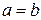эллипсоид можно рассмотреть как поверхность, образованную вращением эллипса вокруг одной из его осей: если эллипсоид образован вращением вокруг его большой оси, он называется вытянутым эллипсоидом вращения, если вокруг меньшей оси – то сжатым эллипсоидом вращения.

В случае 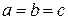имеем сферу.

Уравнение 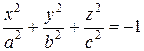, ввиду аналогии с (1) называется уравнением мнимого эллипсоида:

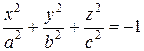(3)

2. Гиперболоид

1. Однополостный.

2. Двухполостный.

Определение. однополостным гиперполоидом называется поверхность, которая в данной декартовой системе координат определяется уравнением:

(4)

Определение. Двухполостным гиперболоидом называется поверхность, определяемая уравнением:

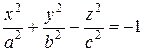(5)

Однополостный гиперболоид

Он задается уравнением (4).

Рассмотрим сечение его координатными плоскостями

Сечение плоскостью 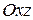(у=0) определяется уравнениями:

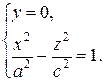
Мы видим, что эта гипербола расположена симметрично относительно осей Ox и Oz и пересекает ось Ox в точках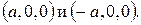

Сечение плоскостью 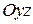(х=0) определяется уравнениями:

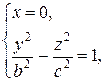- это гипербола, симметричная относительно осей Ox и Oz и пересекает ось 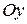в точках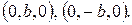

Сечение плоскостью 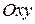(z=0) определяется уравнениями:

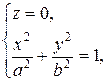- эллипс, который лежит в плоскости . Он называется горловым.

И рассмотрим произвольное сечение плоскостью z=h, параллельной Оху:

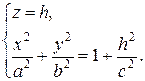
1) Плоскость z=h пересекает гиперболоид (4) по эллипсу с полуосями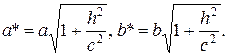

2) Величина 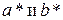имеют наименьшие значения при h=0, т.е. сечение плоскостью z=0.

3) При возрастании 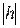величины 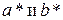бесконечно возрастают.

Построим однополостный гиперболоид:

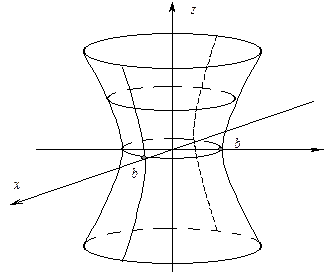
Вывод: однополостный гиперболоид имеет вид бесконечной трубки, бесконечно расширяющейся в обе стороны от горлового эллипса.

Величины 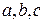называют полуосями однополостного гиперболоида. Полуось с в уравнении (4) стоит со знаком «минус», значит вокруг этой оси происходит вращение гиперболы.

Замечание: В уравнении (4) знак «минус» может стоять и при и при 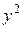, тогда трубка однополостного гиперболоида будет располагаться вокруг ос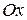и или .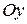

Двухполостный гиперболоид

Задаётся уравнением (5):

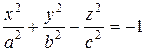(5) Рассмотрим сечение плоскостью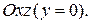

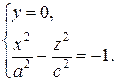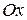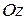- гипербола симметрична осей и и ось 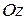пересекает в точках 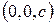и .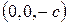

Сечение плоскостью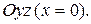

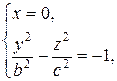- это гипербола, симметричная относительно осей Oу и Oz и пересекает ось 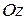в точках 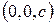и .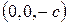

Сечение плоскостью z=h.

(*)

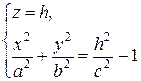
Отсюда видно:

1) 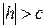, то плоскость пересекает 2-х полостный гиперболоид по эллипсу с полуосями 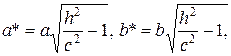симметричному 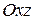и

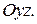
2) При возрастании величины 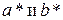возрастают.

3) При убывании 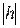величины 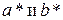убывают и приближаются к нулю при 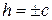, имеем 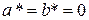Þ эллипс вырождается в точку.

4) При 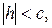система (*) определяют мнимый эллипс, т.е. плоскость z=h с данным гиперболоидом не встречается совсем.

Вывод: Двухполостный гиперболоид есть поверхность, состоящая из двух полостей, каждая имеет вид бесконечной выпуклой чаши, он обладает тремя взаимно перпендикулярными плоскостями симметрии.

Величина 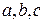называется полуосями двухполостного гиперболоида. Двухполостный гиперболоид можно рассматривать как поверхность, образованную вращением гиперболы вокруг из осей, а именно той, которая гиперболу пересекает.

3. Параболоид

1. Эллиптический параболоид.

2. Гиперболический параболоид.

Эллиптический параболоид

Определение. Эллиптическим параболоидом называется поверхность, которая в декартовой системе координат определяется уравнением:

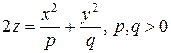(6)

Исследуем эту поверхность методом сечений:

Сечение плоскостью :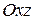

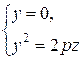- парабола, симметричная относительно оси 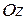, с вершиной в точке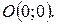

Сечение плоскостью :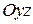

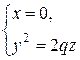- парабола, симметричная оси .

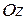Теперь рассмотрим сечение плоскостью, параллельной .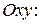

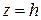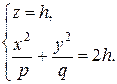
1) При 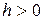плоскость 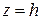пересекает эллиптический параболоид по эллипсу с полуосями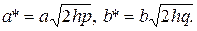

2) При возрастании 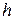величины 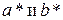возрастают.

3) При убывании 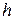величины 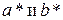убывают. При 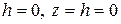вырождается в точку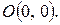

4) При 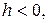будем иметь мнимый эллипс, т.е. плоскость z=h с параболоидом не встречается совсем.

Вывод: Эллиптический параболоид имеет вид выпуклой чаши. Он обладает двумя взаимно перпендикулярными плоскостями симметрии. Точка О называется вершиной эллиптического параболоида. Числа 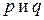называются его параметрами.

Эллиптический параболоид можно рассматривать как вращение параболы вокруг оси z.

Гиперболический параболоид

Определение. Поверхность, которая в ДСК определяется уравнением: 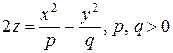(7)

Называется гиперболическим параболоидом.

Исследуем уравнение (7).

Рассмотрим сечение плоскостью 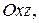т.е. .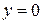

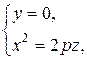- парабола симметрична относительно оси 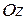с вершнами в начале координат.

Теперь рассмотрим сечения (7) плоскости, параллельной

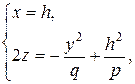- парабола, ветви которой направлены вниз и симметрично относительно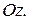

Все эти параболы будут находится вершинами на восходящей параболе 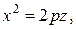и как бы перемещаться вершиной по линии предыдущей параболы.

Сечение гиперболического параболоида плоскостями, параллельными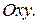

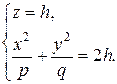- гипербола, симметричная относительно плоскостей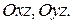

Вывод: Гиперболический параболоид имеет форму седла, обладает двумя взаимно перпендикулярными плоскостями симметрии. Точка, с которой совмещено начало координат называется вершиной гиперболического параболоида. Числа 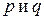называются его параметрами.

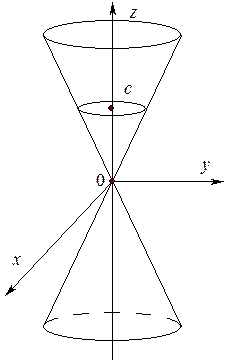
4. Конус

Определение. Поверхность, которая определяется уравнением:

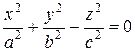(8)

состоит из прямых, проходящих через одну точку, именно, через начало координат и называется конусом.

Заметим, что (8) однородно, все его члены имеют одну и ту же степень 2. Точка .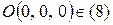

Теорема:Если некоторая точка 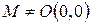лежит на поверхности (8), то все точки прямой, которые проходят через начало координат и точку М, также лежат на этой поверхности.

Прямые, из которых составлен конус, называются его образующими 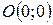- вершина. Проведем сечение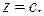

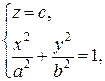- эллипс с полуосями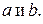

Если 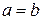, то в сечении окружность и называется круглым конусом.

Рассмотрим уравнение:

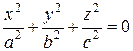(9)

Это уравнение определяет единственную действительную точку 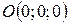. Однако, ввиду аналогии с уравнением (8) его часто называют мнимого конуса.

12 Следующая ⇒