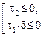- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Алгоритм составления канонического уравнения
Алгоритм составления канонического уравнения
поверхности второго порядка
Пусть в прямоугольной системе координат  поверхность второго порядка описывается уравнением
поверхность второго порядка описывается уравнением
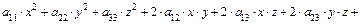
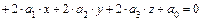 .
.
Требуется определить ее название и составить каноническое уравнение. Для этого нужно выполнить следующие действия:
1. Вычислить ортогональные инварианты
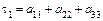 ,
, 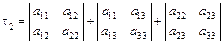 ,
,
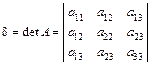 ,
, 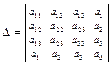 .
.
Если 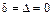 , то вычислить семиинвариант
, то вычислить семиинвариант
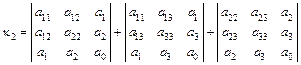 .
.
Если  и
и  , то вычислить семиинвариант
, то вычислить семиинвариант
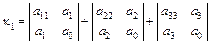 .
.
2. По табл. 11.1 определить название поверхности, а по названию –каноническое уравнение поверхности второго порядка.
3. Составить характеристическое уравнение 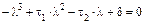 ,
,
используя коэффициенты, вычисленные в п.1, либо разлагая определитель
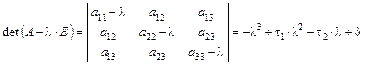 .
.
Найти корни 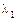 ,
, 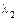 ,
, 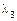 (с учетом кратности) характеристического уравнения.
(с учетом кратности) характеристического уравнения.
4. Занумеровать корни 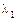 ,
, 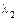 ,
, 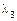 характеристического уравнения в соответствии с правилами:
характеристического уравнения в соответствии с правилами:
а) если поверхность эллиптического типа, то 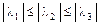 ;
;
б) если поверхность гиперболического типа, то обозначить через 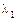 и
и 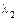 корни одного знака так, чтобы
корни одного знака так, чтобы 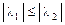 , а через
, а через 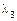 – корень противоположного знака;
– корень противоположного знака;
в) если поверхность параболического типа, то
– если нулевой корень двойной, то 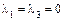 и
и 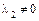 ;
;
– если нулевой корень простой, а ненулевые корни одного знака, то 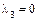 и
и 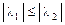 ;
;
– если нулевой корень простой, а ненулевые корни разных знаков, то 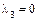 и либо
и либо 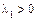 , если
, если 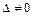 или
или 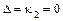 , либо
, либо 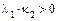 , если
, если 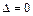 и
и 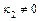 .
.
5. Вычислить коэффициенты канонического уравнения и записать его в канонической системе координат 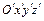 :
:
а) для поверхностей эллиптического типа:
(1) – при 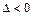 – уравнение эллипсоида
– уравнение эллипсоида 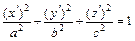 с коэффициентами
с коэффициентами 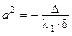 ,
, 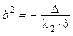 ,
, 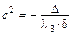 ;
;
Таблица 11.1. Классификация поверхностей второго порядка
| Признаки | Название поверхности | № | |||||||
| Центральные поверхности |
| Эллиптический тип |
|
| Эллипсоид | ||||
|
| Мнимый эллипсоид | ||||||||
|
| Мнимый конус | ||||||||
| Гиперболический тип |
|
| Однополостный гиперболоид | ||||||
|
| Двуполостный гиперболоид | ||||||||
|
| Конус | ||||||||
| Нецентральные поверхности |
| Параболический тип |
| Эллиптический параболоид | |||||
|
| Гиперболический параболоид | ||||||||
|
|
|
| Эллиптический цилиндр | ||||||
|
| Мнимый эллиптический цилиндр | ||||||||
|
| Пара мнимых пересекающихся плоскостей | ||||||||
|
|
| Гиперболический цилиндр | |||||||
|
| Пара пересекающихся плоскостей | ||||||||
|
|
| Параболический цилиндр | |||||||
|
| 
| Пара параллельных плоскостей | |||||||
| Пара мнимых параллельных плоскостей | ||||||||

| Пара совпадающих плоскостей | ||||||||
(2) при 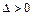 – уравнение мнимого эллипсоида
– уравнение мнимого эллипсоида 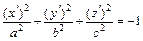 с коэффициентами
с коэффициентами 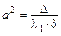 ,
, 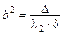 ,
, 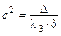 ;
;
(3) при 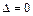 – уравнение мнимого конуса
– уравнение мнимого конуса 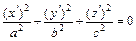 с коэффициентами
с коэффициентами 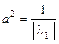 ,
, 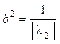 ,
, 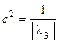 ;
;
б) для поверхностей гиперболического типа:
(4) при 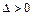 – уравнение однополостного гиперболоида
– уравнение однополостного гиперболоида 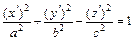 с коэффициентами
с коэффициентами  ,
, 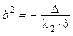 ,
, 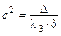 ;
;
(5) при 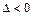 – уравнение двуполостного гиперболоида
– уравнение двуполостного гиперболоида 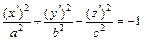 с коэффициентами
с коэффициентами 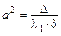 ,
, 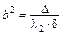 ,
, 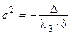 ;
;
(6) при 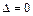 – уравнение конуса
– уравнение конуса 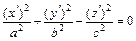 с коэффициентами
с коэффициентами 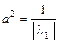 ,
, 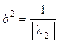 ,
, 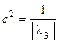 ;
;
в) для поверхностей параболического типа:
(7) при 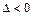 – уравнение эллиптического параболоида
– уравнение эллиптического параболоида 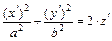 с коэффициентами
с коэффициентами 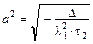 ,
, 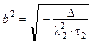 ;
;
(8) при 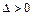 – уравнение гиперболического параболоида
– уравнение гиперболического параболоида 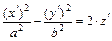 с коэффициентами
с коэффициентами 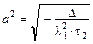 ,
, 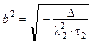 ;
;
(9) при 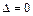 ,
, 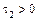 ,
, 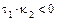 – уравнение эллиптического цилиндра
– уравнение эллиптического цилиндра 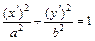 с коэффициентами
с коэффициентами 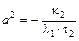 ,
, 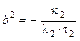 ;
;
(10) при 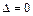 ,
, 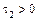 ,
, 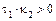 – уравнение мнимого эллиптического цилиндра
– уравнение мнимого эллиптического цилиндра 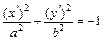 с коэффициентами
с коэффициентами 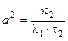 ,
, 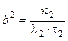 ;
;
(11) при 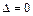 ,
, 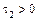 ,
, 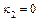 – уравнение пары мнимых пересекающихся плоскостей
– уравнение пары мнимых пересекающихся плоскостей 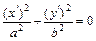 с коэффициентами
с коэффициентами 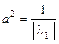 ,
, 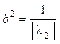 ;
;
(12) при 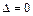 ,
, 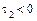 ,
, 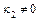 – уравнение гиперболического цилиндра
– уравнение гиперболического цилиндра 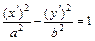 с коэффициентами
с коэффициентами 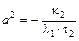 ,
, 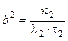 ;
;
(13) при 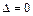 ,
, 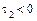 ,
, 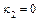 – уравнение пары пересекающихся плоскостей
– уравнение пары пересекающихся плоскостей 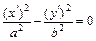 с коэффициентами
с коэффициентами 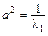 ,
, 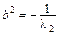 ;
;
(14) при 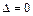 ,
, 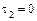 ,
, 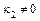 – уравнение параболического цилиндра
– уравнение параболического цилиндра 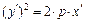 с коэффициентом
с коэффициентом 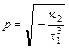 ;
;
(15) при 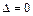 ,
, 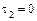 ,
, 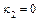 ,
,  – уравнение пары параллельных плоскостей
– уравнение пары параллельных плоскостей  с коэффициентом
с коэффициентом  ;
;
(16) при 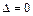 ,
, 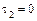 ,
, 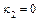 ,
, 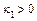 – уравнение пары мнимых параллельных плоскостей
– уравнение пары мнимых параллельных плоскостей 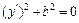 с коэффициентом
с коэффициентом  ;
;
(17) при 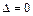 ,
, 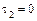 ,
, 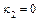 ,
, 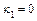 – уравнение пары совпадающих плоскостей
– уравнение пары совпадающих плоскостей 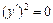 .
.
Пример 11.10. Определить названия и составить канонические уравнения алгебраических поверхностей второго порядка, заданных в прямоугольной системе координат 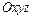 уравнениями:
уравнениями:
а) 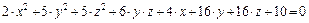 ;
;
б) 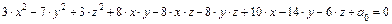 при
при 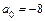 ,
, 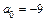 или
или 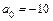 ;
;
в) 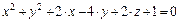 ;
;
г) 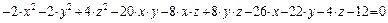 ;
;
д) 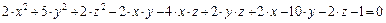 ;
;
е) 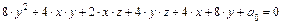 при
при 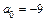 или
или 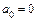 ;
;
ж) 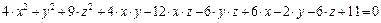 ;
;
з) 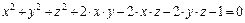 ;
;
и) 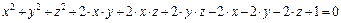 .
.
o а) Определяем коэффициенты уравнения:  ,
, 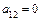 ,
, 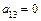 ,
, 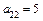 ,
, 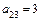 ,
, 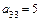 ,
, 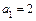 ,
, 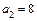 ,
, 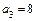 ,
, 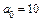 .
.
1. Вычисляем инварианты: 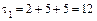 ,
,
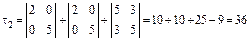 ,
, 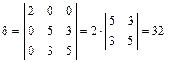 ,
,
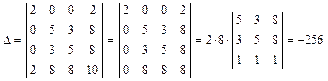 .
.
2. По табл. 11.1 определяем, что уравнение задает эллипсоид, так как 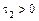 ,
, 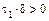 ,
, 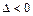 .
.
3. Составляем характеристическое уравнение
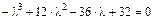
и находим его корни: 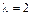 (двойной корень),
(двойной корень), 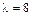 (простой корень).
(простой корень).
4. Поскольку поверхность эллиптического типа, то корни уравнения обозначим 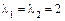 ,
, 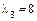 , чтобы выполнялось условие
, чтобы выполнялось условие
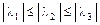 .
.
5. Вычисляем коэффициенты канонического уравнения эллипсоида:
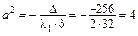 ,
, 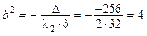 ,
, 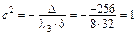 .
.
Таким образом, каноническое уравнение (1) заданной поверхности имеет вид
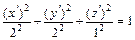 .
.
б) Определяем коэффициенты уравнения: 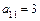 ,
, 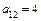 ,
, 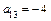 ,
, 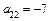 ,
, 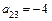 ,
, 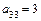 ,
, 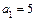 ,
, 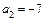 ,
, 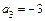 .
.
1. Вычисляем инварианты: 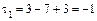 ,
,
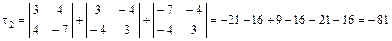 ,
,
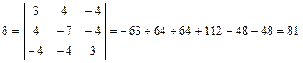 ,
,
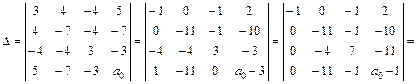
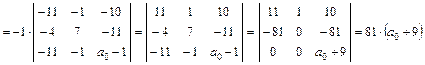 .
.
2. По табл. 11.1 определяем, что уравнение задает поверхность гиперболического типа, так как  . При
. При 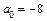 получаем уравнение однополостного гиперболоида, так как
получаем уравнение однополостного гиперболоида, так как 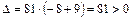 , при
, при 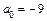 – уравнение конуса, так как
– уравнение конуса, так как  , при
, при 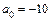 – уравнение двуполостного гиперболоида, так как
– уравнение двуполостного гиперболоида, так как 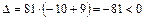 .
.
3. Составляем характеристическое уравнение
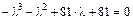
и находим его корни:  ,
, 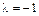 ,
, 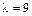 (все корни простые).
(все корни простые).
4. Поскольку поверхность гиперболического типа, то корни уравнения обозначим 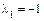 ,
,  , т.е.
, т.е. 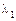 и
и 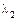 корни одного знака, причем
корни одного знака, причем 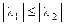 , а
, а  – корень противоположного знака.
– корень противоположного знака.
5. Вычисляем коэффициенты канонического уравнения:
– однополостного гиперболоида (при 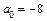
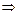
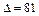 ):
):
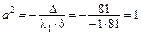 ,
, 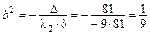 ,
, 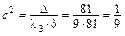 ,
,
следовательно, каноническое уравнение (4) имеет вид
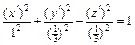 ;
;
– конуса (при 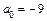 ):
):
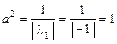 ,
, 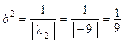 ,
, 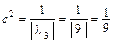 ;
;
следовательно, каноническое уравнение (6) имеет вид
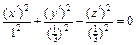 ;
;
– двуполостного гиперболоида (при 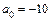
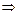
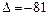 ):
):
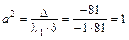 ,
, 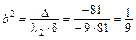 ,
, 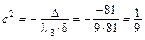 ;
;
следовательно, каноническое уравнение (5) имеет вид
 .
.
в) Определяем коэффициенты уравнения: 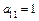 ,
, 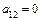 ,
, 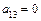 ,
, 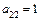 ,
,  ,
, 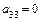 ,
, 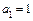 ,
, 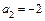 ,
, 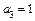 ,
,  .
.
1. Вычисляем инварианты: 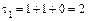 ,
,
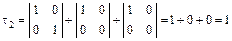 ,
, 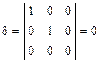 ,
,
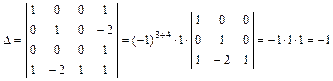 .
.
2. По табл. 11.1 определяем, что уравнение задает эллиптический параболоид, так как 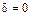 ,
, 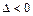 .
.
3. Составляем характеристическое уравнение
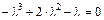
и находим его корни: 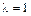 (двойной корень),
(двойной корень), 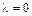 (простой корень).
(простой корень).
4. Поскольку поверхность параболического типа, то корни уравнения обозначим следующим образом: 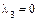 – единственный нулевой корень; так как ненулевые корни одного знака, то
– единственный нулевой корень; так как ненулевые корни одного знака, то 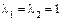 , чтобы выполнялось условие
, чтобы выполнялось условие 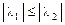 .
.
5. Вычисляем коэффициенты канонического уравнения эллиптического параболоида:
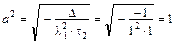 ,
, 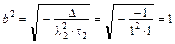 .
.
Таким образом, каноническое уравнение (7) заданной поверхности имеет вид
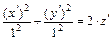 .
.
г) Определяем коэффициенты уравнения: 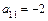 ,
,  ,
, 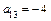 ,
, 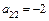 ,
, 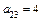 ,
,  ,
, 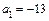 ,
, 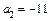 ,
, 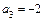 ,
, 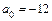 .
.
1. Вычисляем инварианты: 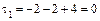 ,
,
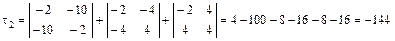 ,
,
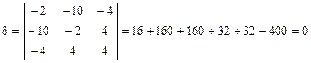 ,
,
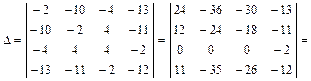
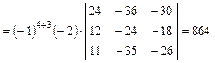 .
.
2. По табл. 11.1 определяем, что уравнение задает гиперболический параболоид, так как 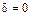 ,
, 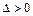 .
.
3. Составляем характеристическое уравнение 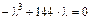 и находим его корни:
и находим его корни: 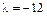 ,
, 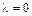 ,
, 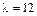 (все корни простые).
(все корни простые).
4. Поскольку поверхность параболического типа, то корни характеристического уравнения обозначим следующим образом: 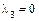 – единственный нулевой корень; так как ненулевые корни разных знаков и
– единственный нулевой корень; так как ненулевые корни разных знаков и 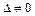 , то
, то 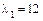 , тогда
, тогда 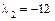 .
.
5. Вычисляем коэффициенты канонического уравнения гиперболического параболоида:
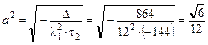 ,
, 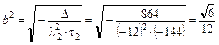 .
.
Таким образом, каноническое уравнение (8) заданной поверхности имеет вид
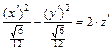 .
.
д) Определяем коэффициенты уравнения: 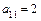 ,
, 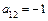 ,
, 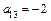 ,
, 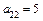 ,
, 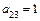 ,
, 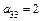 ,
, 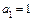 ,
, 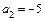 ,
, 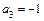 ,
, 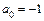 .
.
1. Вычисляем инварианты: 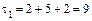 ,
,
 ,
,
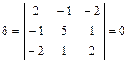 ,
, 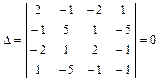 .
.
Так как 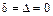 , то вычисляем семиинвариант:
, то вычисляем семиинвариант:
 .
.
2. По табл. 11.1 определяем, что уравнение задает эллиптический цилиндр, так как 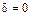 ,
, 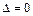 ,
, 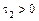 ,
, 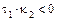 .
.
3. Составляем характеристическое уравнение  и находим его корни:
и находим его корни: 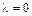 ,
, 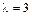 ,
, 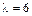 (все корни простые).
(все корни простые).
4. Поскольку поверхность параболического типа, то корни уравнения обозначим следующим образом: 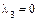 – единственный нулевой корень; так как ненулевые корни одного знака, то
– единственный нулевой корень; так как ненулевые корни одного знака, то 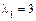 ,
, 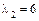 , чтобы выполнялось условие
, чтобы выполнялось условие 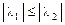 .
.
5. Вычисляем коэффициенты канонического уравнения эллиптического цилиндра:
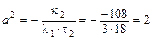 ,
, 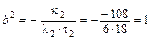 .
.
Таким образом, каноническое уравнение (9) заданной поверхности имеет вид
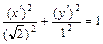 .
.
е) Определяем коэффициенты уравнения: 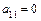 ,
, 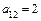 ,
, 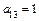 ,
, 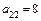 ,
, 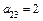 ,
, 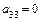 ,
, 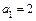 ,
, 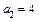 ,
, 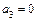 .
.
1. Вычисляем инварианты: 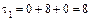 ,
,
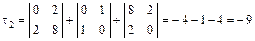 ,
,
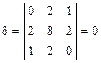 ,
, 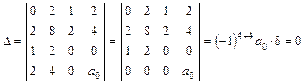 .
.
Так как 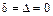 , то вычисляем семиинвариант:
, то вычисляем семиинвариант:
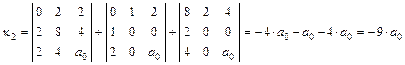 .
.
2. По табл. 11.1 определяем, что уравнение задает поверхность параболического типа, так как 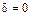 . При
. При 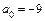 получаем уравнение гиперболического цилиндра, так как
получаем уравнение гиперболического цилиндра, так как 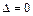 ,
, 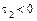 ,
, 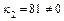 ; при
; при 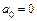 – уравнение пары пересекающихся плоскостей, так как
– уравнение пары пересекающихся плоскостей, так как 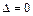 ,
, 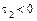 ,
, 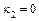 .
.
3. Составляем характеристическое уравнение
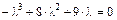
и находим его корни: 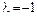 ,
, 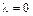 ,
, 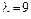 (все корни простые).
(все корни простые).
4. Поскольку поверхность параболического типа, то корни характеристического уравнения обозначим следующим образом: 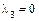 – единственный нулевой корень; так как ненулевые корни разных знаков и
– единственный нулевой корень; так как ненулевые корни разных знаков и 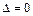 , то
, то 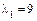 , тогда
, тогда 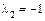 (при
(при 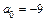 имеем
имеем 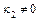 и
и 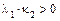 , а при
, а при 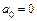 имеем
имеем 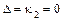 ).
).
5. Вычисляем коэффициенты канонического уравнения:
– гиперболического цилиндра (при 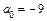
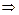
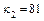 ):
):
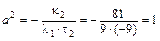 ,
, 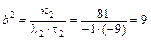 ;
;
следовательно, каноническое уравнение (12) имеет вид
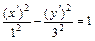 ;
;
– пары пересекающихся плоскостей (при 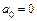
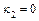 ):
):
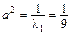 ,
, 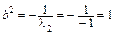 ;
;
следовательно, каноническое уравнение (13) имеет вид
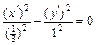 .
.
ж) Определяем коэффициенты уравнения: 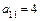 ,
, 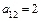 ,
, 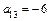 ,
, 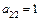 ,
, 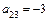 ,
, 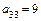 ,
, 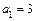 ,
, 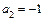 ,
, 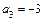 ,
, 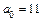 .
.
1. Вычисляем инварианты: 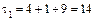 ,
,
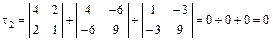 ,
, 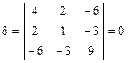 ,
,
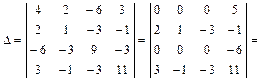
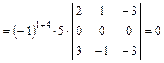 .
.
Так как 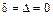 , то вычисляем
, то вычисляем
 .
.
2. По табл. 11.1 определяем, что уравнение задает параболический цилиндр, так как 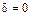 ,
, 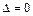 ,
, 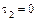 ,
, 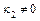 .
.
3. Составляем характеристическое уравнение 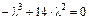 и находим его корни:
и находим его корни: 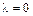 (двойной корень),
(двойной корень), 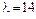 (простой корень).
(простой корень).
4. Поскольку поверхность параболического типа, то корни уравнения обозначим следующим образом: 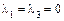 – двойной нулевой корень, а
– двойной нулевой корень, а 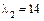 – ненулевой корень.
– ненулевой корень.
5. Вычисляем коэффициент канонического уравнения параболического цилиндра:
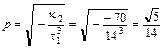 .
.
Таким образом, каноническое уравнение (14) заданной поверхности имеет вид
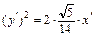 .
.
з) Определяем коэффициенты уравнения: 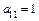 ,
, 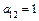 ,
, 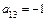 ,
, 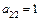 ,
, 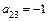 ,
, 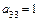 ,
, 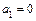 ,
, 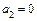 ,
, 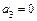 ,
, 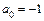 .
.
1. Вычисляем инварианты: 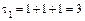 ,
,
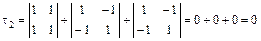 ,
,
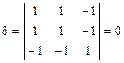 ,
, 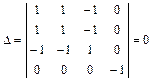 .
.
Так как 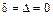 , то вычисляем
, то вычисляем
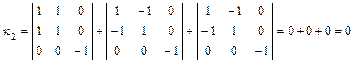 .
.
Так как 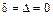 и
и 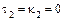 , то вычисляем
, то вычисляем
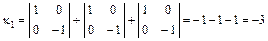 .
.
2. По табл. 11.1 определяем, что уравнение задает пару параллельных плоскостей, так как 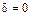 ,
, 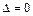 ,
, 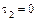 ,
, 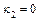 ,
, 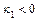 .
.
3. Составляем характеристическое уравнение 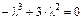 и находим его корни:
и находим его корни: 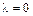 (двойной корень),
(двойной корень), 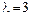 (простой корень).
(простой корень).
4. Поскольку поверхность параболического типа, то корни уравнения обозначим следующим образом: 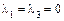 – двойной нулевой корень, а
– двойной нулевой корень, а 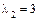 – ненулевой корень.
– ненулевой корень.
5. Вычисляем коэффициент канонического уравнения пары параллельных плоскостей:
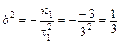 .
.
Таким образом, каноническое уравнение (15) заданной поверхности имеет вид
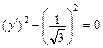 .
.
и) Определяем коэффициенты уравнения: 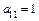 ,
, 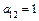 ,
, 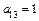 ,
, 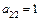 ,
, 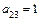 ,
, 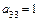 ,
, 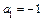 ,
, 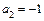 ,
, 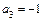 ,
, 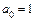 .
.
1. Вычисляем инварианты: 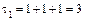 ,
,
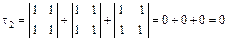 ,
,
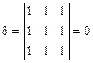 ,
, 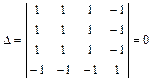 .
.
Так как 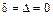 , то вычисляем
, то вычисляем
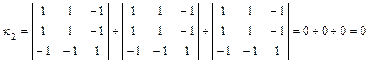 .
.
Так как 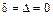 и
и 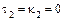 , то вычисляем
, то вычисляем
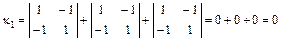 .
.
2. По табл. 11.1 определяем, что уравнение задает пару совпадающих плоскостей, так как 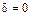 ,
, 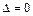 ,
, 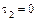 ,
, 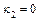 ,
, 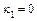 .
.
3. Составляем характеристическое уравнение 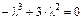 и находим его корни:
и находим его корни: 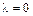 (двойной корень),
(двойной корень), 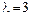 (простой корень).
(простой корень).
4. Поскольку поверхность параболического типа, то корни уравнения обозначим следующим образом: 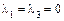 – двойной нулевой корень, а
– двойной нулевой корень, а 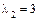 – ненулевой корень.
– ненулевой корень.
5. Записываем каноническое уравнение (17) пары совпадающих плоскостей:
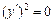 . n
. n
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|