поверхности второго порядка. Классификация поверхностей второго порядка. Канонические уравнения поверхностей второго порядка

11.3. поверхности второго порядка

11.3.1. Классификация поверхностей второго порядка

Алгебраической поверхностьювторого порядка называется геометрическое место точек пространства, которое в какой-либо аффинной системе координат может быть задано уравнением вида

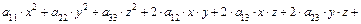
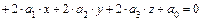где старшие коэффициенты 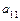, , 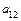, , 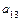, 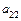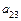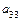не равны нулю одновременно. Без ограничения общности можно считать, что система координат, в которой задано уравнение поверхности второго порядка, прямоугольная. Для каждой поверхности второго порядка существует прямоугольная система координат , в которой уравнение принимает наиболее простой (канонический) вид. Она называется канонической, а уравнение – каноническим.

Канонические уравнения поверхностей второго порядка

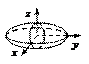
1. – уравнение эллипсоида;

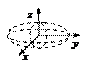
2. 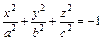– уравнение мнимого эллипсоида;

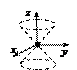
3. 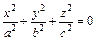– уравнение мнимого конуса;

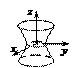
4. 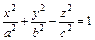– уравнение однополостного

гиперболоида;

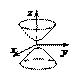
5. 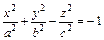– уравнение двуполостного

гиперболоида;

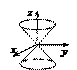
6. 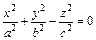– уравнение конуса;

7. 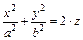– уравнение эллиптического

параболоида;

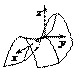
8. – уравнение гиперболического

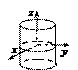параболоида;

9. 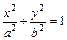– уравнение эллиптического

цилиндра;

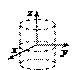
10. 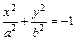– уравнение мнимого

эллиптического цилиндра;

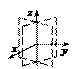
11. 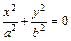– уравнение пары мнимых

пересекающихся плоскостей;

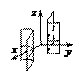12. 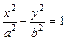– уравнение гиперболического

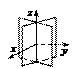цилиндра;

13. 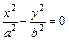– уравнение пары пересекающихся

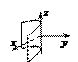плоскостей;

14. 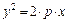– уравнение параболического

цилиндра;

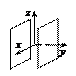
15. 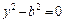– уравнение пары параллельных

плоскостей;

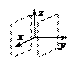
16. 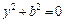– уравнение пары мнимых

параллельных плоскостей;

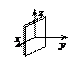
17. 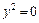– уравнение пары совпадающих

плоскостей.

В этих уравнениях , , 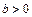, , 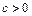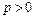причем 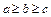в уравнениях п.1–3; 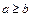в уравнениях п.4–7,9–11.

Поверхности (1),(4)–(9), (12)–(15),(17) называются вещественными (действительными), а поверхности (2),(3),(10),(11),(16) – мнимыми. Вещественные поверхности изображены в канонических системах координат. Изображения мнимых поверхностей даются штриховыми линиями только для иллюстрации.

Поверхность второго порядка называется центральной, если она имеет единственный центр (симметрии). В противном случае, если центр отсутствует или не является единственным, поверхность называется нецентральной. К центральным поверхностям относятся эллипсоиды (вещественный и мнимый), гиперболоиды (однополостный и двуполостный), конусы (вещественный и мнимый). Остальные поверхности – нецентральные.

12 Следующая ⇒