Контрольно-графическая работа. Исходные данные и условия решения задач. Особенности построения

1 Контрольно-графическая работа

Контрольно-графическая работа состоит из четырех задач, выполненных на листах форматов А3(А2). Листы ватмана располагаются в горизонтальном положении с размещением на них по две задачи согласно приложения В. Масштаб изображения 2:1 (исходные данные увеличиваются в два раза).

1.1 Исходные данные и условия решения задач

Исходные данные задач выбираются согласно таблицы 1 Приложения А в зависимости от варианта задания.

Требуется решить следующие задачи:

Задача №1. Построить проекции точек пересечения прямой а с поверхностью.

Задача №2. Построить проекции линии пересечения поверхностей способом вспомогательных секущих плоскостей.

Задача №3. Построить проекции линии пересечения поверхностей способом вспомогательных концентрических сфер.

Задача №4. Построить полную развёртку поверхности с нанесением на ней точек или линии пересечения поверхностей.

1.2 Особенности построения

1 Линией пересечения поверхностей в общем случае является:

- при пересечении кривых поверхностей - пространственная кривая линия (рисунок 1а);

- при пересечении кривой поверхности с гранной поверхностью – пространственная замкнутая кривая линия с изломами в точках пересечения рёбер гранной поверхности с кривой поверхностью (рисунок 1б).

а) б)

Рисунок 1 – Варианты контуров линий пересечения

а) кривых поверхностей;

б) кривой и гранной поверхностей

2 Опорными точками на линии пересечения поверхностей, как правило, являются точки, нахождение которых в задачи не требует каких-либо вспомогательных построений.

Характерными точками называются точки, определяющие характер линии пересечения (точки излома линии пересечения, точки на очерке поверхности и т.д.).

Точками видимости называются точки, лежащие на линии пересечении поверхностейв местах пересечения с границей видимости. Они разграничивают видимую часть линии пересечения от невидимой.

3 Если основание прямого кругового конуса расположено под наклоном к какой-либо плоскости проекций, то в этой плоскости оно спроецируется в эллипс. На рисунке 2 показан один из способов построения эллипса, при условии, что основание конуса наклонено к плоскости П₁ и показано определение положения границы видимости конуса для плоскости П₁.

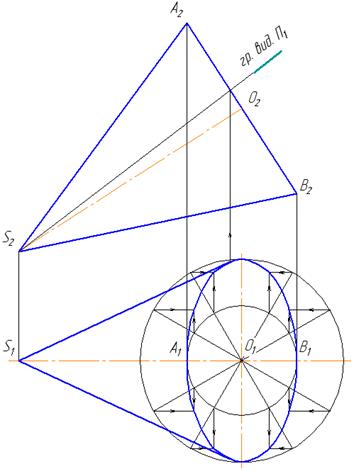
Рисунок 2 - Построение эллипса и определение границы видимости конуса

⇐ Предыдущая 123 4 5 6 7 Следующая ⇒