Главная

Контакты

Случайная статья

• Автоматизация
• Антропология
• Археология
• Архитектура
• Биология
• Ботаника
• Бухгалтерия
• Военная наука
• Генетика
• География
• Геология
• Демография
• Деревообработка
• Журналистика
• Зоология
• Изобретательство
• Информатика
• Искусство
• История
• Кинематография
• Компьютеризация
• Косметика
• Кулинария
• Культура
• Лексикология
• Лингвистика
• Литература
• Логика
• Маркетинг
• Математика
• Материаловедение
• Медицина
• Менеджмент
• Металлургия
• Метрология
• Механика
• Музыка
• Науковедение
• Образование
• Охрана Труда
• Педагогика
• Полиграфия
• Политология
• Право
• Предпринимательство
• Приборостроение
• Программирование
• Производство
• Промышленность
• Психология
• Радиосвязь
• Религия
• Риторика
• Социология
• Спорт
• Стандартизация
• Статистика
• Строительство
• Технологии
• Торговля
• Транспорт
• Фармакология
• Физика
• Физиология
• Философия
• Финансы
• Химия
• Хозяйство
• Черчение
• Экология
• Экономика
• Электроника
• Электротехника
• Энергетика

Понятие поверхности второго порядка.

Содержание.

· Понятие поверхности второго порядка.

1. Инварианты уравнения поверхности второго порядка.

· Классификация поверхностей второго порядка.

1. Классификация центральных поверхностей.

Ä 1°. Эллипсоид.

Ä 2°. Однополостный гиперболоид.

Ä 3°. Двуполостный гиперболоид.
Ä 4°. Конус второго порядка.

2. Классификация нецентральных поверхностей.

Ä 1°. Эллиптический цилиндр, гиперболический цилиндр, эллиптический параболоид, гиперболиче­ский параболоид.

Ä 2°. Параболический цилиндр

• Исследование формы поверхностей второго порядка по их каноническим уравнениям.

1. Эллипсоид.
2. Гиперболоиды.

Ä 1°. Однополостный гиперболоид.

Ä 2°. Двуполостный гиперболоид.

3. Параболоиды.

Ä 1°. Эллиптический параболоид.
Ä 2°. Гиперболический пара­болоид.

4. Конус и цилиндры второго порядка.

Ä 1°. Конус второго порядка.
Ä 2°. Эллиптический цилиндр.
Ä 3°. Гиперболический цилиндр.
Ä 4°. Параболический цилиндр.

Список использованной литературы.

1. «Аналитическая геометрия» В.А. Ильин, Э.Г. Позняк

§ 1. Понятие поверхности второго порядка.

Поверхность второго порядка - геометрическое место точек, декартовы прямоугольные координаты которых удовлетворяют уравнению вида

a₁₁х² + а₂₂у² + a₃₃z²+ 2a₁₂xy + 2a₂₃уz + 2a₁₃xz + 2а₁₄ x + 2а₂₄у+2а₃₄z +а₄₄ =0 (1)

в котором по крайней мере один из коэффициентов a₁₁ , а₂₂ , a₃₃ , a₁₂ , a_{23 ,}a₁₃ отличен от нуля.

Уравнение (1) мы будем называть общим уравнением по­верхности второго порядка.

Очевидно, поверхность второго порядка, рассматриваемая как геометрический объект, не меняется, если от данной де­картовой прямоугольной системы координат перейти к другой декартовой системе координат. Отметим, что исходное уравне­ние (1) и уравнение, полученное после преобразования коор­динат, алгебраически эквивалентны.

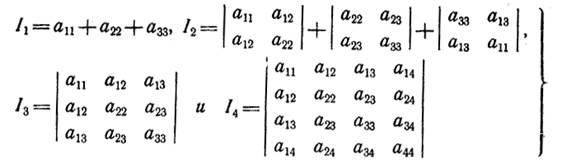
1. Инварианты уравнения поверхности второго порядка.

Справедливо следующее утверждение.

являются инвариантами уравнения (1) поверхности второго-порядка относительно преобразований декартовой системы ко­ординат.

Доказательство этого утверждения приведено в выпуске «Линейная алгебра» настоящего курса.