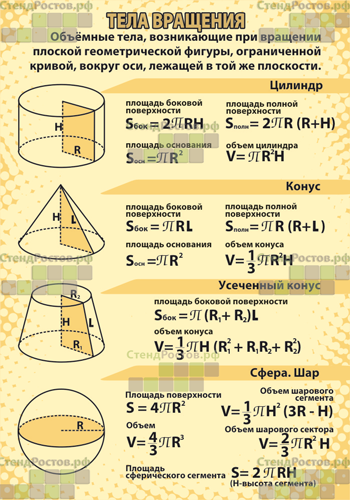
ПРАКТИЧЕСКАЯ РАБОТА №1. Объём куба и прямоугольного параллелепипеда.. Теоретическая часть. Куб - это такой параллелепипед, у которого все ребра равны, поэтому все его грани - квадраты.

Задание:Повторить формулы для вычисления многогранников и тел вращения, вспомнить основные понятия, характеризующие данные фигуры.

Построить многогранники и тела вращения в тетради и записать основные формулы (материал взять в данных таблицах). Решить задачи, используя записанные формулы.

Выполнить практическую работу:

ПРАКТИЧЕСКАЯ РАБОТА №1

Объём куба и прямоугольного параллелепипеда.

Цель:закрепить навык решения практических задач на вычисление объёмов куба и прямоугольного

параллелепипеда.

Теоретическая часть

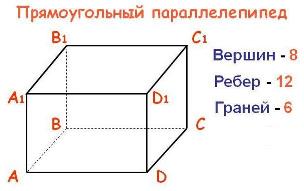Многогранники могут иметь самую различную форму. Среди них выделяют параллелепипеды. Обычный, всем известный кирпич с точки зрения геометрии является параллелепипедом. Форму параллелепипеда имеют многие предметы, с которыми мы встречаемся в жизни, например коробки, используемые для упаковки различных товаров.

· У параллелепипеда 8 вершин, 12 ребер и 6 граней.

· Каждая грань параллелепипеда - прямоугольник.

· Противоположные грани параллелепипеда равны.

Каждый параллелепипед имеет три измерения: длину, ширину и высоту.
Среди всех параллелепипедов особую роль играет - куб.

Куб - это такой параллелепипед, у которого все ребра равны, поэтому все его грани - квадраты.

За единицу измерения объема принимается объем единичного куба, т.е. объем куба, длина ребра которого равна 1 единице длины.

1 кубический сантиметр (1 cм³)- объем куба, длина которого равна 1 см.
1 кубический дециметр (1 дм³)- объем куба, длина которого равна 1 дм.
1 кубический метр (1 м³)- объем куба, длина которого равна 1 м.

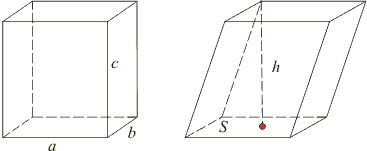
Теорема: объем прямоугольного параллелепипеда с измерениями а, b, с вычисляется по формуле

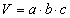, V = S_осн h.

Теорема: объем наклонного (любого) параллелепипеда равен произведению площади основания S на высоту h:

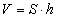Объем куба равен кубу (третьей степени) его ребра. V = a³

Пример 1. Найдите объем параллелепипеда, измерения которого равны 6 мм, 10 мм и 15 мм.

Решение: 6 x 10 x 15 = 900 (мм³).

Пример 2.Найдите объем куба, ребро которого равно 5 дм.
Решение: 5³ = 5 x 5 x 5 = 125 (дм³).
Заметим, что единица объема, равная одному кубическому дециметру, имеет и другое название - литр.В литрах обычно измеряют объемы жидкостей и сыпучих веществ.

12 Следующая ⇒