Контакты

Случайная статья

Логарифмические неравенства. Практическая часть. Вариант 2 Вариант. Вариант 4 Вариант. Вариант

⇐ ПредыдущаяСтр 2 из 2

Логарифмические неравенства

Решение логарифмических неравенств основано на свойстве логарифмической функции: функция возрастает, если основание больше 1, и убывает, если 0 < а < 1.

Пример 4 - Решим неравенство 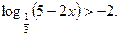Решение.

Число -2 равно 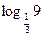. Поэтому данное неравенство можно переписать в виде

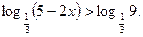Логарифмическая функция с основанием 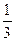определена и убывает на множестве положительных чисел. Следовательно, второму неравенству удовлетворяют такие числа х, для которых выполняется условие

0 < 5-2x < 9, откуда -2 < x < 2,5.

Ответ: (-2; 2,5).

Практическая часть

1 Вариант 2 Вариант

Решить уравнение и неравенство: Решить уравнение и неравенство:

1) 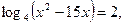1)

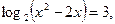
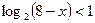2) 2)

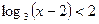
3 Вариант 4 Вариант

Решить уравнение и неравенство: Решить уравнение и неравенство:

1) 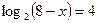; 1)

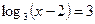
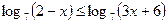2) 2)

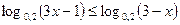
5 Вариант

Решить уравнение и неравенство:

1)

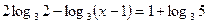
2)

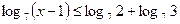
Контрольные вопросы

1 Понятие логарифмического уравнения.

2 Свойство логарифмической функции, на котором основано решение логарифмических неравенств.

3 Свойства логарифмов.

Список использованных источников

1. Н. В. Богомолов. Математика, задачи с решениями. – М.: Дрофа, 2018.

2. Н. В. Богомолов. Сборник дидактических заданий по математике. – М.: Дрофа, 2018.

3. Н. В. Богомолов, П. И. Самойленко. Математика. - М.: Дрофа, 2017.

⇐ Предыдущая 12

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.