Теоретическое обоснование. Логарифмические уравнения

Стр 1 из 2Следующая ⇒

Инструкционная карта

для выполнения практической работы

Тема: Решение логарифмических уравнений и неравенств

Цель работы:

- научиться решать простейшие логарифмические уравнения и неравенства.

Теоретическое обоснование

Логарифмические уравнения

Определение - Логарифмическим уравнением называется такое уравнение, в котором неизвестное содержится под знаком логарифма (в частности, в основании логарифма).

При решении таких уравнений обе части уравнения представляют в виде логарифмов с одинаковым основанием. У равных логарифмов с равными основаниями логарифмируемые выражения равны. После решения такого уравнения необходимо выполнить проверку.

Пример 1 - Решить уравнение .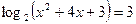

Решение.

По определению логарифма 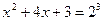, то есть ,

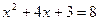или 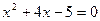. Корнями данного квадратного уравнения являются числа -5 и 1. Следовательно, эти числа являются корнями логарифмического уравнения.

Ответ: -5; 1.

Пример 2 - Решить уравнение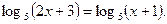

Решение.

Это уравнение определено для тех значений х, при которых выполненынеравенства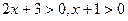 . Для этих х данное уравнение равносильно уравнению 2х +3 = х+1. Отсюда х = -2. Однако, число х = -2 не удовлетворяет неравенству х+1 > 0.Следовательно, данное уравнение корней не имеет.

Пример 3 - Решить уравнение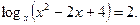

Решение.

Этому уравнению удовлетворяют все числа, больше 0, и отличные от 1, при условии, что справедливо равенство 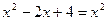, то есть -2х + 4 = 0, откуда х = 2.

Ответ: 2.

12 Следующая ⇒