Основная часть. Дополнительные задачи. ДММ. Типовой вариант контрольной работы. темы 1 – 4 программы)

Стр 1 из 2Следующая ⇒

Линеная алгебра

Математический анализ. Типовой вариант зачетной контрольной работы (2 модуль)

Основная часть

ЗАДАЧА 1. Найдите предел .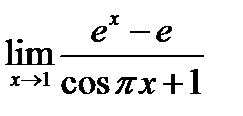

ЗАДАЧА 2.Докажите, используя определение предела функции в точке, что функция 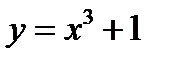непрерывна в точке .

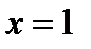ЗАДАЧА 3.Укажите для функции 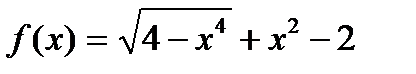эквивалентную функцию вида 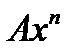при .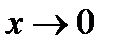

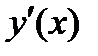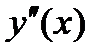ЗАДАЧА 4.Найдите производные и функции 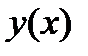, заданной параметрически: .

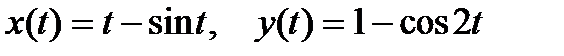ЗАДАЧА 5.Исследуйте на экстремум функцию .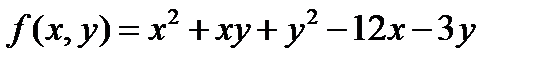

ЗАДАЧА 6.Найдите экстремум функции 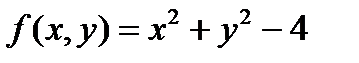при условии 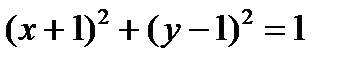с помощью функции Лагранжа. Нарисуйте: а) график условия; б) изолинии, проходящие через стационарные точки функции Лагранжа; в) градиент в этих точках.

ЗАДАЧА 7.Спрос 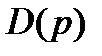и предложение 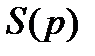зависят от цены 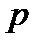следующим образом: 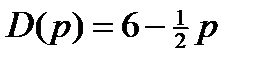, 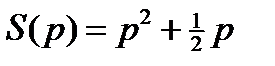. Найдите наибольшее значение дохода и определите эластичность функции дохода в точке максимума.

Дополнительные задачи

ЗАДАЧА 8.Докажите, что производная по направлению градиента функции 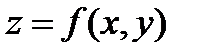в точке 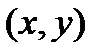максимальна.

ЗАДАЧА 9.Докажите сходимость последовательности 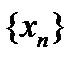, где .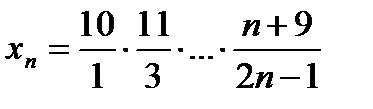

ЗАДАЧА 10.Найдите значения 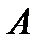и B, при которых функция 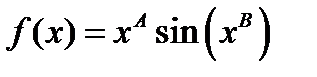является бесконечно малой при .

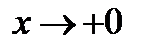ДММ. Типовой вариант контрольной работы

(темы 1 – 4 программы)

1. Докажите, что .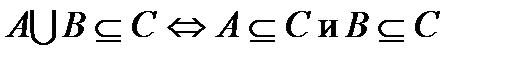

2. Пусть 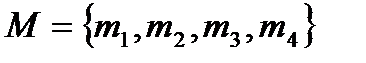, 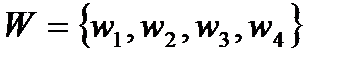и предпочтения участников имеют вид:

; ;

; .

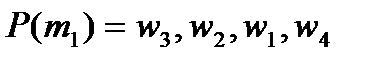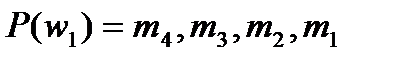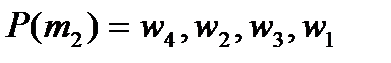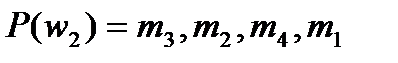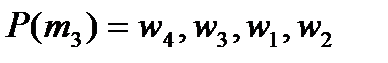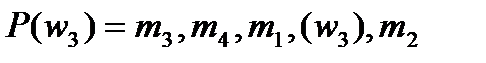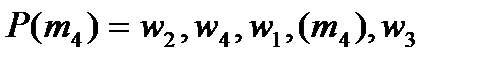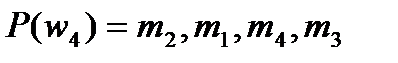Является ли устойчивым паросочетание

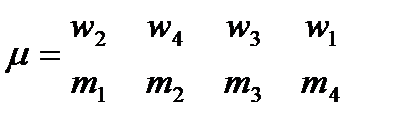Ответ обоснуйте.

3. Пусть 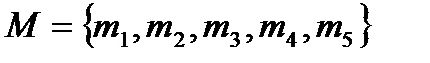, 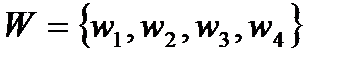и предпочтения участников имеют вид:

; ;

; .

;

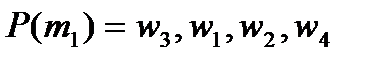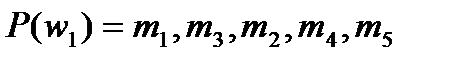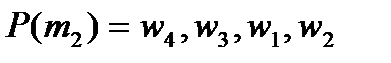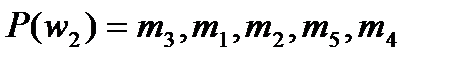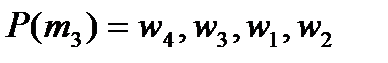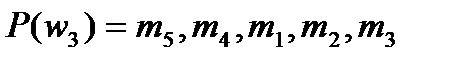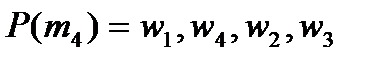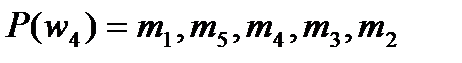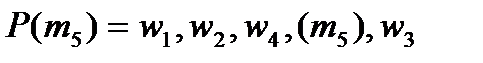Постройте паросочетания 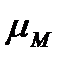и .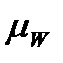

4. Пусть А – непустое конечное множество, на котором задана функция полезности 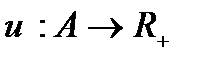- множество неотрицательных действительных чисел. Бинарное отношение Р определим так, что 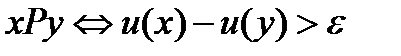, где 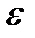- фиксированное положительное число. Какими свойствами обладает бинарное отношение Р?

5. Докажите, что бинарное отношение Р транзитивно, если и только если .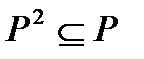

6. Приведите пример, показывающий, что отношение несравнимости для антирефлексивного

связного полутранзитивного отношения не всегда удовлетворяет условию связности.

7. Постройте мажоритарный граф при следующих предпочтениях участников на множестве 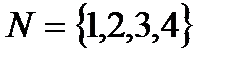относительно кандидатов из множества :

;

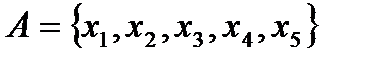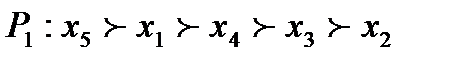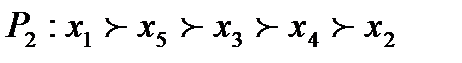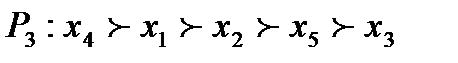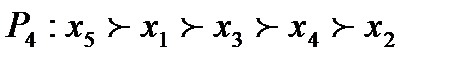Есть ли здесь победитель Кондорсе? Проанализируйте полученный результат.

8. Компания из трех человек выбирает вариант совместного проведения вечернего досуга. Ими рассматриваются четыре альтернативы: поход на дискотеку (D), поход в кино (С), поход в театр (Т), поход на модное фотобиеннале (F). Предпочтения участников имеют вид:


D C F T	C D F T	T F C D

Какое коллективное решение будет получено, если применить максиминную процедуру? Какой результат даст применение минимаксной процедуры?

Микроэкономика.

12 Следующая ⇒