Как составить уравнения касательной плоскости и нормали в точке, если поверхность задана явной функцией ?

Как составить уравнения касательной плоскости и нормали в точке, если поверхность задана явной функцией ?

Перепишем её в неявном виде :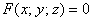

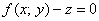и по тем же принципам найдём частные производные:

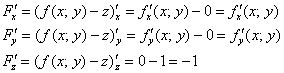
Таким образом, формула касательной плоскости 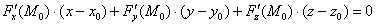трансформируется в следующее уравнение:

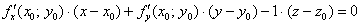, и соответственно, канонические уравнения нормали:

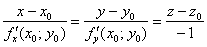
Как нетрудно догадаться, 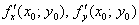– это уже «настоящие» частные производные функции двух переменных в точке 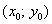, которые мы привыкли обозначать буквой «зет» и находили 100500 раз.

Заметьте, что в данной статье достаточно запомнить самую первую формулу, из которой в случае необходимости легко вывести всё остальное (понятно, обладая базовым уровнем подготовки). Именно такой подход следует использовать в ходе изучения точных наук, т.е. из минимума информации надо стремиться «вытаскивать» максимум выводов и следствий. «Соображаловка» и уже имеющиеся знания в помощь! Этот принцип полезен ещё и тем, что с большой вероятностью спасёт в критической ситуации, когда вы знаете очень мало.

Отработаем «модифицированные» формулы парой примеров:

Пример 4

Составить уравнения касательной плоскости и нормали к поверхности 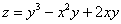в точке .

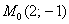Небольшая тут накладка получилась с обозначениями – теперь буква 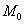обозначает точку плоскости 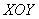, но что поделать – такая уж популярная буква….

Решение: уравнение искомой касательной плоскости составим по формуле:

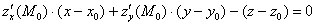
Вычислим значение функции в точке :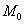

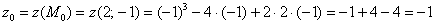
Вычислим частные производные 1-го порядка в данной точке:

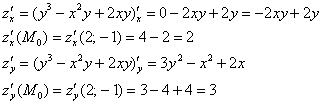
Таким образом:

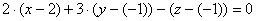
аккуратно, не спешим:

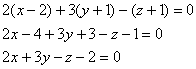
Запишем канонические уравнения нормали в точке :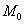

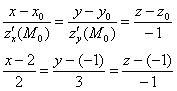
Ответ: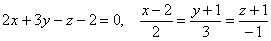

И заключительный пример для самостоятельного решения:

Пример 5

Составить уравнения касательной плоскости и нормали к поверхности 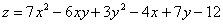в точке .

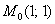Заключительный – потому, что фактически все технические моменты я разъяснил и добавить особо нечего. Даже сами функции, предлагаемые в данном задании, унылы и однообразны – почти гарантированно на практике вам попадётся «многочлен», и в этом смысле Пример №2 с экспонентой смотрится «белой вороной». Кстати, гораздо вероятнее встретить поверхность, заданную уравнением 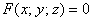и это ещё одна причина, по которой функция 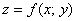вошла в статью «вторым номером».

И напоследок обещанный секрет: так как же избежать зубрёжки определений? (я, конечно, не имею в виду ситуацию, когда студент что-то лихорадочно зубрит перед экзаменом)

Определение любого понятия/явления/объекта, прежде всего, даёт ответ на следующий вопрос: ЧТО ЭТО ТАКОЕ? (кто/такая/ такой/такие). Осознанно отвечая на данный вопрос, вы должны постараться отразить существенные признаки, однозначно идентифицирующие то или иное понятие/явление/объект. Да, поначалу это получается несколько косноязычно, неточно и избыточно (препод поправит =)), но со временем развивается вполне достойная научная речь.

⇐ Предыдущая 12