
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Как найти уравнения касательной плоскости и нормали к поверхности в заданной точке?
Как найти уравнения касательной плоскости и нормали к поверхности в заданной точке?
Сегодня на уроке я расскажу вам об одном популярном приложении дифференциального исчисления функции двух переменных, а именно, о том, что вы видите в заголовке. По существу, это «пространственный аналог» задачи нахождения касательной и нормали к графику функции  одной переменной, и поэтому никаких трудностей возникнуть не должно.
одной переменной, и поэтому никаких трудностей возникнуть не должно.
Начнём с базовых вопросов: ЧТО ТАКОЕ касательная плоскость и ЧТО ТАКОЕ нормаль? Многие осознают эти понятия на уровне интуиции. Самая простая модель, приходящая на ум – это шар, на котором лежит тонкая плоская картонка. Картонка расположена максимально близко к сфере и касается её в единственной точке. Кроме того, в точке касания она закреплена торчащей строго вверх иголкой.
В теории существует довольно остроумное определение касательной плоскости. Представьте произвольную поверхность 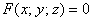 и принадлежащую ей точку
и принадлежащую ей точку  . Очевидно, что через точку
. Очевидно, что через точку 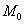 проходит много пространственных линий, которые принадлежат данной поверхности. У кого какие ассоциации? =) …лично я представил осьминога. Предположим, что у каждой такой линии существует пространственная касательная в точке
проходит много пространственных линий, которые принадлежат данной поверхности. У кого какие ассоциации? =) …лично я представил осьминога. Предположим, что у каждой такой линии существует пространственная касательная в точке 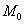 .
.
Определение 1: касательная плоскость к поверхности в точке 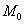 – это плоскость, содержащая касательные ко всем кривым, которые принадлежат данной поверхности и проходят через точку
– это плоскость, содержащая касательные ко всем кривым, которые принадлежат данной поверхности и проходят через точку 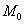 .
.
Определение 2: нормаль к поверхности в точке 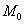 – это прямая, проходящая через данную точку перпендикулярно касательной плоскости.
– это прямая, проходящая через данную точку перпендикулярно касательной плоскости.
Просто и изящно. Кстати, чтобы вы не померли со скуки от простоты материала, чуть позже я поделюсь с вами одним изящным секретом, который позволяет РАЗ И НАВСЕГДА забыть о зубрёжке различных определений.
С рабочими формулами и алгоритмом решения познакомимся прямо на конкретном примере. В подавляющем большинстве задач требуется составить и уравнение касательной плоскости, и уравнения нормали:
Пример 1
Найти уравнения касательной плоскости и нормали к поверхности  в точке
в точке  .
.
Решение:если поверхность задана уравнением 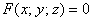 (т.е. неявно), то уравнение касательной плоскости к данной поверхности в точке
(т.е. неявно), то уравнение касательной плоскости к данной поверхности в точке  можно найти по следующей формуле:
можно найти по следующей формуле:
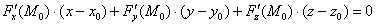
Особое внимание обращаю на необычные частные производные  – их не следует путать с частными производными неявно заданной функции (хотя поверхность задана неявно). При нахождении этих производных нужно руководствоваться правилами дифференцирования функции трёх переменных, то есть, при дифференцировании по какой-либо переменной, две другие буквы считаются константами:
– их не следует путать с частными производными неявно заданной функции (хотя поверхность задана неявно). При нахождении этих производных нужно руководствоваться правилами дифференцирования функции трёх переменных, то есть, при дифференцировании по какой-либо переменной, две другие буквы считаются константами:

Не отходя от кассы, найдём частную производную в точке:

Аналогично:

Это был самый неприятный момент решения, в котором ошибка если не допускается, то постоянно мерещится. Тем не менее, здесь существует эффективный приём проверки, о котором я рассказывал на уроке Производная по направлению и градиент.
Все «ингредиенты» найдены и теперь дело за аккуратной подстановкой с дальнейшими упрощениями:

 – общее уравнение искомой касательной плоскости.
– общее уравнение искомой касательной плоскости.
Настоятельно рекомендую проконтролировать и этот этап решения. Сначала нужно убедиться, что координаты точки касания  действительно удовлетворяют найденному уравнению:
действительно удовлетворяют найденному уравнению:

 – верное равенство.
– верное равенство.
Теперь «снимаем» коэффициенты 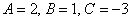 общего уравнения плоскости и проверяем их на предмет совпадения либо пропорциональности с соответствующими значениями
общего уравнения плоскости и проверяем их на предмет совпадения либо пропорциональности с соответствующими значениями  . В данном случае пропорциональны. Как вы помните из курса аналитической геометрии,
. В данном случае пропорциональны. Как вы помните из курса аналитической геометрии,  – это вектор нормали касательной плоскости, и он же – направляющий вектор нормальной прямой. Составим канонические уравнения нормали по точке
– это вектор нормали касательной плоскости, и он же – направляющий вектор нормальной прямой. Составим канонические уравнения нормали по точке  и направляющему вектору
и направляющему вектору  :
:

В принципе, знаменатели можно сократить на «двойку», но особой надобности в этом нет
Ответ: 
Уравнения не возбраняется обозначить какими-нибудь буквами, однако, опять же – зачем? Здесь и так предельно понятно, что к чему.
Следующие два примера для самостоятельного решения. Небольшая «математическая скороговорка»:
Пример 2
Найти уравнения касательной плоскости и нормали к поверхности  в точке
в точке  .
.
И задание, интересное с технической точки зрения:
Пример 3
Составить уравнения касательной плоскости и нормали к поверхности 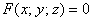 в точке
в точке 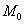
 в точке
в точке  .
.
Тут есть все шансы не только запутаться, но и столкнуться с трудностями при записи канонических уравнений прямой. А уравнения нормали, как вы, наверное, поняли, принято записывать именно в таком виде. Хотя, по причине забывчивости либо незнания некоторых нюансов более чем приемлема и параметрическая форма.
Примерные образцы чистового оформления решений в конце урока.
В любой ли точке поверхности существует касательная плоскость? В общем случае, конечно же, нет. Классический пример – это коническая поверхность  и точка
и точка  – касательные в этой точке непосредственно образуют коническую поверхность, и, разумеется, не лежат в одной плоскости. В неладах легко убедиться и аналитически:
– касательные в этой точке непосредственно образуют коническую поверхность, и, разумеется, не лежат в одной плоскости. В неладах легко убедиться и аналитически:  .
.
Другим источником проблем является факт несуществования какой-либо частной производной в точке. Однако это ещё не значит, что в данной точке нет единой касательной плоскости.
Но то была, скорее, научно-популярная, нежели практически значимая информация, и мы возвращаемся к делам насущным:
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|