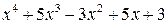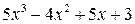- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Задачи для самостоятельного решения.
.
Если использовать для определения коэффициентов А, В, С метод частных значений х, нужно в тождественное равенство числителей
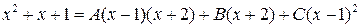
подставить удобные в данном случае значения х=1, х=-2 и ещё одно любое значение, например, х=0. В результате получим равенства для неопределённых коэффициентов:
при х=1: 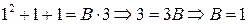 ;
;
при х=-2: 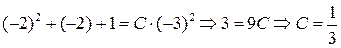 ;
;
при х=0: 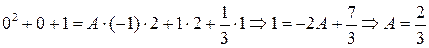 .
.
Итак, получили разложение подынтегральной дроби на сумму простых дробей:
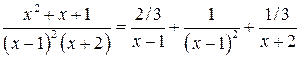 .
.
Вычисляем данный интеграл как сумму интегралов от простых дробей:
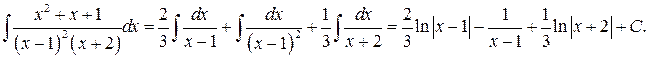
----------------------------------------------------------------------------------------------------------------
Интегрирование рациональных функций. Стр. 3
4. Интегралы вида 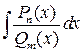 , где
, где 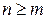 , разбиваются на сумму двух интегралов. Подынтегральная функция первого слагаемого равна неполному частному от деления
, разбиваются на сумму двух интегралов. Подынтегральная функция первого слагаемого равна неполному частному от деления 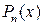 на
на 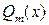 . Подынтегральная функция второго слагаемого представляет собой дробь, числитель которой равен остатку от деления
. Подынтегральная функция второго слагаемого представляет собой дробь, числитель которой равен остатку от деления 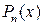 на
на 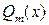 , а знаменатель совпадает с
, а знаменатель совпадает с 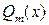 .
.
Пример 4. Найти интеграл 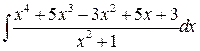 .
.
Решение. Выполним деление:
|
| 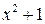
| ||
|
| 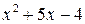
| ||
|
| |||
|
| |||
|
| 
| ||
|
| 
| ||
|
| 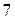
| ||
Разложим исходный интеграл на сумму двух интегралов, согласно указанному выше правилу:
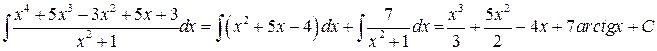 .
.
Задачи для самостоятельного решения.
1. ; 2. ; 3. ; 4. ;
5. ; 6. .
Домашнее задание.
1. ; 2. ; 3. ; 4. .
----------------------------------------------------------------------------------------------------------------
Интегрирование рациональных функций. Стр. 4
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|