
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Интегрирование рациональных функций.
Интегрирование рациональных функций.
1. Интегралы вида 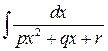 путём выделения полного квадрата в знаменателе подынтегрального выражения сводится к одному из двух интегралов:
путём выделения полного квадрата в знаменателе подынтегрального выражения сводится к одному из двух интегралов:
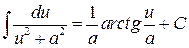 (1)
(1)
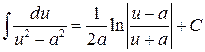 (2),где
(2),где 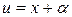 .
.
Пример 1. Найти интеграл 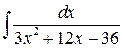 .
.
Решение. 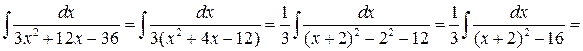
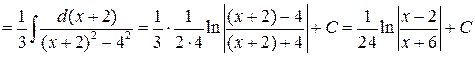 .
.
2. Интегралы вида  сводятся к интегралу (1) или (2) и интегралу
сводятся к интегралу (1) или (2) и интегралу 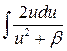 , который можно вычислить с помощью замены
, который можно вычислить с помощью замены  . Что разбить исходный интеграл на два более простых, числитель подынтегрального выражения представляют в виде суммы (разности) двух выражений, одно из которых совпадает с производной знаменателя.
. Что разбить исходный интеграл на два более простых, числитель подынтегрального выражения представляют в виде суммы (разности) двух выражений, одно из которых совпадает с производной знаменателя.
Пример 2. Найти интеграл 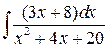 .
.
Решение. а) Вычисляем производную знаменателя подынтегрального выражения:
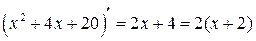 ;
;
б) разобьём числитель подынтегрального выражения на сумму, одно из слагаемых которой равно 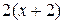 :
:
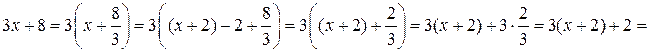
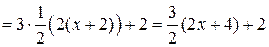 ;
;
в) представим исходный интеграл в виде суммы двух интегралов:
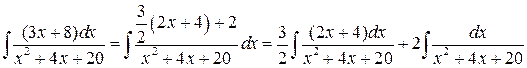 ;
;
г) вычислим каждый из полученных интегралов:
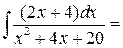
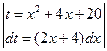
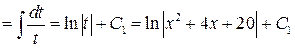 ;
;
;
----------------------------------------------------------------------------------------------------------------
Интегрирование рациональных функций. Стр. 1
д) запишем ответ с учётом коэффициентов, стоящих перед интегралами:
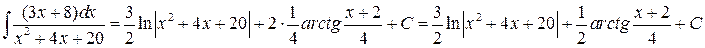
3. Нахождение интегралов вида 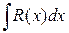 , где
, где  - правильная рациональная дробь, т.е.
- правильная рациональная дробь, т.е. 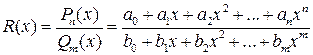 (
( 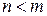 ), основано на разложении рациональной дроби на сумму простых (элементарных) дробей, т.е. дробей вида
), основано на разложении рациональной дроби на сумму простых (элементарных) дробей, т.е. дробей вида
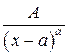 ;
;  ,
,
где 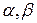 - натуральные числа,
- натуральные числа, 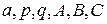 - действительные числа,
- действительные числа, 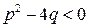 (корни трёхчлена являются комплексными числами).
(корни трёхчлена являются комплексными числами).
Перед интегрированием рациональной дроби 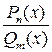 надо сделать следующие преобразования и вычисления:
надо сделать следующие преобразования и вычисления:
а)Разложить знаменатель правильной рациональной дроби на линейные множители и квадратичные множители, не имеющие действительных корней: 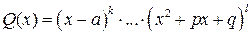 , причём
, причём 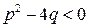 .
.
б)Правильную рациональную дробь разложить на сумму простых дробей:
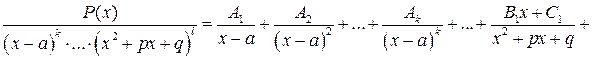
 , где
, где 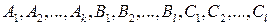 - это неопределённые коэффициенты, которые находятся из условия тождественного равенства по х между правильной рациональной дробью и суммой простых дробей.
- это неопределённые коэффициенты, которые находятся из условия тождественного равенства по х между правильной рациональной дробью и суммой простых дробей.
в)Вычислить неопределенные коэффициенты, для этого
· привести простые дроби к общему знаменателю;
· приравняв числители равных дробей, имеющих равные знаменатели, получить тождественное равенство двух целых многочленов;
· приравнивая коэффициенты при одинаковых степенях x в тождественно равных многочленах, получить и решить систему уравнений для неопределённых коэффициентов.
Вместо приравнивания коэффициентов при одинаковых степенях х можно использовать метод частных значений х, суть которого состоит в том, что тождественно равные многочлены принимают одинаковые значения при любых конкретных значениях х, поэтому достаточно подставить в равенство числителей несколько удобных значений х и получить в результате уравнения для неопределённых коэффициентов. На практике можно комбинировать метод частных значений х с приравниванием коэффициентов при одинаковых степенях х.
----------------------------------------------------------------------------------------------------------------
Интегрирование рациональных функций. Стр. 2
Пример 3. Найти интеграл 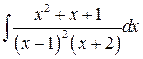 .
.
Решение. Т.к. знаменатель дроби разложен на множители, то сразу выполним разложение подынтегральной функции на сумму простых дробей:
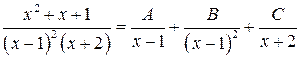 .
.
Приводим к общему знаменателю сумму простых дробей:
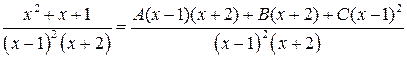 .
.
Приравниваем числители дробей, имеющих одинаковые знаменатели:
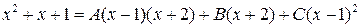 .
.
Раскроем в правой части равенства скобки и сгруппируем слагаемые по степеням х:
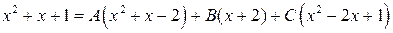 ;
;
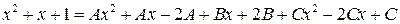 ;
;
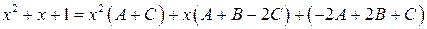 .
.
Приравнивая коэффициенты при одинаковых степенях х, получаем и решаем систему уравнений относительно коэффициентов А, В, С:
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|